摘要:6.在正三棱柱中.为上的点.当= 时.使得. 例2正方形的四边上分别取四点.便得.把正方形沿对角线折起.如图: (1)求证:是矩形, (2)当二面角为多大的.为正方形. 例3 在直三棱柱中..为棱BB上一点...为的中点. (1) 若为线段上(不同于)的任意一点.求证:. (2) 试问:若.在线段上的点能否使与平面成角?证明你的结论. 例 4在三棱锥中.两两垂直.若与平面所成角为.与平面所成角为.且.则当.为何值时.三棱锥的体积最大.最大值是多少? 例5如图.三棱柱的底面是边长为2的等边三角形.侧面是的菱形.且平面面ABC.M是上的动点 (1) 当M为的中点时.求证: (2) 试求二面角的平面角最小时.三棱锥的体积 高三数学第二轮复习教学案 第三课时 立体的综合运用 班级 学号 姓名 [教学目标] 能够解决空间角.距离及与探索问题相关的综合性问题. [例题讲解] 例题1 (1)若二面角为.直线.则所在平面内的直线与所成角的取值范围 ( ) A ) B C D (2)在半径为的球内有一内接正三棱锥.它的底面三个顶点恰好都在同一个大圆上.一个动点从三棱锥的一个顶点出发沿球面运动.经过其余三点后返回.则经过的最短路程是 ( ) A B C D (3)正四面体ABCD的棱长为1.G是底面的中心.M在线段上且使.则GM的长为 ( ) A B C D (4)在直三棱柱中..E.F分别为.的中点.沿棱柱的表面从E到F两点的最短路径的长度为 ( ) A B C D (5)正方体ABCD-的棱长为1.在正方体表面上与点A距离是的点的轨迹的长度为 . (6)在直角坐标系中.设.沿轴将直角坐标系折成的二面角后.AB的长度是 . 例2已知四棱锥的底面为直角梯形..PA⊥底面.且是PB的中点 (1)证明:面面 (2)求与所成的角 (3)求面与面所成二面角的大小 例3中...D为AC的中点.E为BD的中点.AE的延长线交BC与F.将沿BD折起.二面角为 (1) 求证:面面 (2) 为何值时. 例4 斜三棱柱中.底面是边长为的正三角形.且点A1在底面的射影O恰是BC的中点 (1) 当侧棱与底面成角时.求二面角的大小 (2) D为侧棱上一点.当为何值时. (3) 对于(2)中的点D.若面.求C到面的距离 例5 如图.在长方体中..点E在棱AB上移动 (1) 证明: (2) 当E为AB的中点时.求点E到面的距离 (3) AE为何值时.二面角的大小为.
网址:http://m.1010jiajiao.com/timu3_id_513199[举报]
在正三棱柱ABC-A1B1C1中,AB=2,AA1=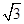 ,点D为AC的中点,点E在线段AA1上.
,点D为AC的中点,点E在线段AA1上.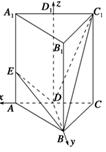
(1)当AE∶EA1=1∶2时,求证DE⊥BC1;
(2)是否存在点E,使二面角D-BE-A等于60°,若存在求AE的长;若不存在,请说明理由.
在正三棱柱ABC-A1B1C1中,AB=2,AA1=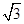 ,点D为AC的中点,点E在线段AA1上.
,点D为AC的中点,点E在线段AA1上.
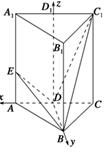
(1)当AE∶EA1=1∶2时,求证DE⊥BC1;
(2)是否存在点E,使二面角D-BE-A等于60°,若存在求AE的长;若不存在,请说明理由.
 ,点D为AC的中点,点E在线段AA1上.
,点D为AC的中点,点E在线段AA1上.
(1)当AE∶EA1=1∶2时,求证DE⊥BC1;
(2)是否存在点E,使二面角D-BE-A等于60°,若存在求AE的长;若不存在,请说明理由.
 如图,在正三棱柱ABC-A1B1C1中,点D在边BC上,AD⊥C1D.
如图,在正三棱柱ABC-A1B1C1中,点D在边BC上,AD⊥C1D.(Ⅰ)求证:AD⊥平面BC C1B1;
(Ⅱ)设E是B1C1上的一点,当
| B1E | EC1 |

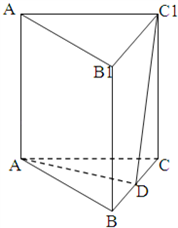
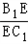 的值为多少时,A1E∥平面ADC1?请给出证明。
的值为多少时,A1E∥平面ADC1?请给出证明。