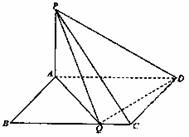
摘要：在矩形ABCD.AB=1.BC=.PA⊥平面ABCD.若在BC边上只有一个点Q.满足PQ⊥QD.则= ．
网址：http://m.1010jiajiao.com/timu3_id_512928[举报]
如图，矩形ABCD，|AB|=1，|BC|=a，PA⊥平面ABCD，|PA|=1。
（1）BC边上是否存在点Q，使得PQ⊥QD，并说明理由；
（2）若BC边上存在唯一的点Q使得PQ⊥QD，指出点Q的位置,并求出此时AD与平面PDQ所成的角的正弦值；
（3）在（2）的条件下，求二面角Q ―PD―A的正弦值。
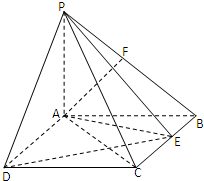如图，PA⊥平面ABCD，四边形ABCD是矩形，PA=AB=1，PD与平面ABCD所成角是30°，点F是PB的中点，点E在矩形ABCD的边BC上移动．（Ⅰ）证明：无论点E在边BC的何处，都有PE⊥AF；
（Ⅱ）当CE等于何值时，二面角P-DE-A的大小为45°． 查看习题详情和答案>>
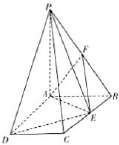如图，PA⊥平面ABCD，ABCD是矩形，PA=AB=1，PD与平面ABCD所成角是30°，点F中PB的中点，点E在边BC上移动．（1）证明：PE⊥AF；
（2）当CE=
| 2 |
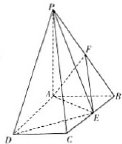如图，PA⊥平面ABCD，ABCD是矩形，PA=AB=1，PD与平面ABCD所成角是30°，点F中PB的中点，点E在边BC上移动．
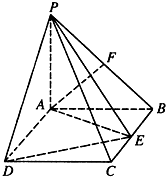如图，PA⊥平面ABCD，四边形ABCD为矩形，PA=AB=