摘要:椭圆的左.右焦点为.P在椭圆上.且.则= .
网址:http://m.1010jiajiao.com/timu3_id_512523[举报]
椭圆C1:
+
=1(a>b>0)的左右顶点分别为A、B.点P双曲线C2:
-
=1在第一象限内的图象上一点,直线AP、BP与椭圆C1分别交于C、D点.若△ACD与△PCD的面积相等.
(1)求P点的坐标;
(2)能否使直线CD过椭圆C1的右焦点,若能,求出此时双曲线C2的离心率,若不能,请说明理由. 查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
(1)求P点的坐标;
(2)能否使直线CD过椭圆C1的右焦点,若能,求出此时双曲线C2的离心率,若不能,请说明理由. 查看习题详情和答案>>
椭圆
+
=1(a>b>0)的左、右焦点分别为F1、F2,点P在椭圆上,∠F1PF2=60°,设
=λ
(I)当λ=2时,求椭圆离心率e;
(II)当椭圆离心率最小时,PQ为过椭圆右焦点F2的弦,且|PQ|=
,求椭圆的方程.
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| |PF1| |
| |PF2| |
(I)当λ=2时,求椭圆离心率e;
(II)当椭圆离心率最小时,PQ为过椭圆右焦点F2的弦,且|PQ|=
| 16 |
| 5 |
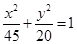 上有一点P,
上有一点P,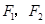 是椭圆的左、右焦点,
是椭圆的左、右焦点,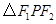 为直角三角形,则这样的点P有( )
为直角三角形,则这样的点P有( )