摘要:弦长公式.但计算焦点弦长时可运用定义“曲线上的点到焦点的距离与到相应准线的距离之比等于离心率 以简化弦长计算,
网址:http://m.1010jiajiao.com/timu3_id_512462[举报]
直线与圆相交时,求弦长,你有哪些计算方法?常规方法的缺点是计算量较大,但思路清晰;那联立直线方程和圆的方程,你能通过不解方程而利用根与系数的关系及两点间的距离公式来进行计算吗?再想一下,圆又有哪些几何性质?特别是半径、弦心距与半弦长构成的三角形是什么三角形,你能利用它来进行快速地计算吗?
已知椭圆C:
+
=1(a>b>0),过焦点且垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形.
(Ⅰ)求椭圆的方程; (Ⅱ)过点Q(-1,0)的直线l交椭圆于A,B两点,交直线x=-4于点E,且
=λ
,
=μ
.求证:λ+μ为定值,并计算出该定值.
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
(Ⅰ)求椭圆的方程; (Ⅱ)过点Q(-1,0)的直线l交椭圆于A,B两点,交直线x=-4于点E,且
| AQ |
| QB |
| AE |
| EB |
(理科)已知椭圆C:
+
=1(a>b>0),过焦点且垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形.
(1)求椭圆的方程;
(2)过点Q(-1,0)的直线l交椭圆于A,B两点,交直线x=-4于点E,且
=λ
,
=μ
.求证:λ+μ为定值,并计算出该定值.
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆的方程;
(2)过点Q(-1,0)的直线l交椭圆于A,B两点,交直线x=-4于点E,且
| AQ |
| QB |
| AE |
| EB |
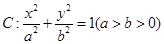 ,过焦点且垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形.
,过焦点且垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形.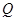
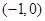 的直线
的直线 交椭圆于
交椭圆于 两点,交直线
两点,交直线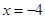 于点
于点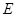 ,且
,且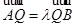 ,
, ,
,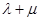 为定值,并计算出该定值.
为定值,并计算出该定值.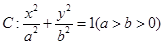 ,过焦点且垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形.
,过焦点且垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形.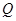
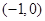 的直线
的直线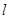 交椭圆于
交椭圆于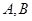 两点,交直线
两点,交直线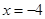 于点
于点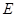 ,且
,且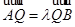 ,
,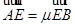 ,
,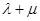 为定值,并计算出该定值.
为定值,并计算出该定值.