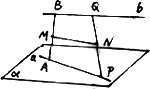
摘要:已知.是两条异面直线.AB是其公垂线.垂足分别是A.B.M∈.N∈.AB=4.AM=3.BN=2.MN=.则与所成的角为 . 例题讲解 例1.如图.在三棱锥D-ABC中.DA⊥平面ABC.∠ACB=90°.∠ABD=30°.AC=BC.求异面直线AB与CD所成角的余弦值. 例2.如图.正三棱柱ABC-A1B1C1的底面边长为8.对角线B1C=10.D为AC中点. (1)求证:AB1∥平面C1BD,(2)求异面直线AB1与BC1所成的角. 例3.如图.在直四棱柱ABCD-A1B1C1D1中.底面是边长为1的菱形.侧棱长为2. (1)B1D1与A1D能否垂直?请证明你的判断. (2)当∠A1B1C1在上变化时.求异面直线AC1与A1B1所成角的取值范围. 课后作业 班级 学号 姓名
网址:http://m.1010jiajiao.com/timu3_id_512333[举报]
(1)设l1、l2是两条异面直线,其公垂线段AB上的单位向量为n,又C、D分别是l1、l2上任意一点,求证:| |=|
|=| ·n|;
·n|;
(2)已知正方体ABCD—A1B1C1D1的棱长为a,求体对角线BD1与面对角线B1C的距离.?
查看习题详情和答案>>
(1)设l1、l2是两条异面直线,其公垂线段AB上的单位向量为n,又C、D分别是l1、l2上任意一点,求证: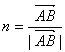 ;
;
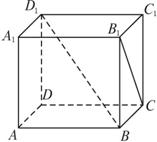
(2)已知正方体ABCD—A1B1C1D1的棱长为a,求体对角线BD1与面对角线B1C的距离.
查看习题详情和答案>>
(1)设l1、l2是两条异面直线,其公垂线段AB上的单位向量为n,又C、D分别是l1、l2上任意一点,求证: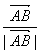
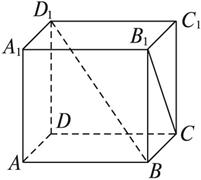
(2)已知正方体ABCD—A1B1C1D1的棱长为a,求体对角线BD1与面对角线B1C的距离.
查看习题详情和答案>>