题目内容
(1)设l1、l2是两条异面直线，其公垂线段AB上的单位向量为n,又C、D分别是l1、l2上任意一点，求证：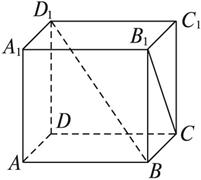
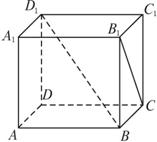
(2)已知正方体ABCD—A1B1C1D1的棱长为a,求体对角线BD1与面对角线B1C的距离.
(1)证明：∵n=,
∴
·n=
由于CA⊥AB，BD⊥AB,
∴
因此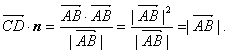
(2)解：先找一个向量n,它既与BD1垂直，又与B1C垂直.设n=
,其中λ、μ为待定的数.
由
=-a2-λa2+μa2=-a2(1+λ-μ)=0,∴1+λ-μ=0.
又由
=-a2-μa2=0,
∴1+μ=0.
于是解得μ=-1,λ=-2,∴n=
,
|n|=
又BC是连结这两条异面直线BD1与B1C上的任意点的线段，由第(1)题知所求距离为
绿色通道：(1)在以上推导中，我们已暗中假定了n的方向是由l1上的点A指向l2上的点B，而
的方向也是由l1上的点C指向l2上的点D，这样求得
是正值.如果n指向与
指向不同，则
是负值，所以一般地就写成
.又如果n不是单位向量，则
(2)
、
、
有着基底的作用，我们将BD1与B1C的公垂线段向量n用这组基底来表示.因为相差一个常数因子不影响其公垂性，所以设定了n=
，使其只含有两个待定常数，这样就方便多了.
练习册系列答案
相关题目
|=|
·n|;
;