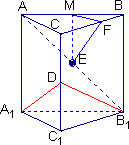
摘要:在正三棱柱ABC-A1B1C1中.BC=.D.E分别为棱CC1.A1B1的中点.E在平面ABD内的射影G是△ABD的重心 (1)求该棱柱的高, (2)求直线EA与直线BC所成的角.
网址:http://m.1010jiajiao.com/timu3_id_512125[举报]
如图,在直三棱柱ABC-A1B1C1中,AA1=2,∠ABC=90°AB=1;点D、E分别在![]() 上,且B1E⊥A1D,四棱锥C-ABDA1与直三棱柱的体积之比为3∶5.■
上,且B1E⊥A1D,四棱锥C-ABDA1与直三棱柱的体积之比为3∶5.■
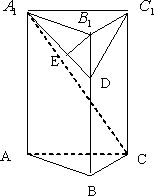
(1)求异面直线DE与B1C1的距离;
(2)若BC=![]() ,求二面角A1-DC1-B1的平面角的正切值.
,求二面角A1-DC1-B1的平面角的正切值.
如图,在直三棱柱ABC-A1B1C1中,AB=AC=5,D、E分别为BC、BB1的中点,四边形B1BCC1是边长为6的正方形.

(Ⅰ)求证:A1B∥平面AC1D;
(Ⅱ)求证:CE⊥平面AC1D;
(Ⅲ)求二面角C-AC1-D的余弦值.