摘要:设.是两个不等的正数.且.求证:.
网址:http://m.1010jiajiao.com/timu3_id_512098[举报]
已知各项均为正数的两个无穷数列{an}、{bn}满足anbn+1+an+1bn=2nan+1(n∈N*).
(Ⅰ)当数列{an}是常数列(各项都相等的数列),且b1=
时,求数列{bn}的通项公式;
(Ⅱ)设{an}、{bn}都是公差不为0的等差数列,求证:数列{an}有无穷多个,而数列{bn}惟一确定;
(Ⅲ)设an+1=
(n∈N*),Sn=
bi,求证:2<
<6.
查看习题详情和答案>>
(Ⅰ)当数列{an}是常数列(各项都相等的数列),且b1=
| 1 |
| 2 |
(Ⅱ)设{an}、{bn}都是公差不为0的等差数列,求证:数列{an}有无穷多个,而数列{bn}惟一确定;
(Ⅲ)设an+1=
| 2an2+an |
| an+1 |
| 2n |
 |
| i=1 |
| Sn |
| n2 |
已知各项均为正数的两个无穷数列{an}、{bn}满足anbn+1+an+1bn=2nan+1(n∈N*).
(Ⅰ)当数列{an}是常数列(各项都相等的数列),且b1= 时,求数列{bn}的通项公式;
时,求数列{bn}的通项公式;
(Ⅱ)设{an}、{bn}都是公差不为0的等差数列,求证:数列{an}有无穷多个,而数列{bn}惟一确定;
(Ⅲ)设an+1= ,Sn=
,Sn=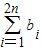 ,求证:2<
,求证:2<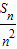 <6.
<6.
查看习题详情和答案>>
(Ⅰ)当数列{an}是常数列(各项都相等的数列),且b1=
 时,求数列{bn}的通项公式;
时,求数列{bn}的通项公式;(Ⅱ)设{an}、{bn}都是公差不为0的等差数列,求证:数列{an}有无穷多个,而数列{bn}惟一确定;
(Ⅲ)设an+1=
 ,Sn=
,Sn=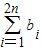 ,求证:2<
,求证:2<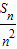 <6.
<6.查看习题详情和答案>>
本题设有(1)、(2)、(3)三个选考题,每题7分,请考生任选2题做答,满分14分
(1)选修4-2:矩阵与变换
变换 是将平面上每个点
是将平面上每个点 的横坐标乘
的横坐标乘 ,纵坐标乘
,纵坐标乘 ,变到点
,变到点 .
.
(Ⅰ)求变换 的矩阵;
的矩阵;
(Ⅱ)圆 在变换
在变换 的作用下变成了什么图形?
的作用下变成了什么图形?
(2)选修4-4:坐标系与参数方程
已知极点与原点重合,极轴与x轴的正半轴重合.若曲线 的极坐标方程为:
的极坐标方程为: ,直线
,直线 的参数方程为:
的参数方程为: (
( 为参数).
为参数).
(Ⅰ)求曲线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)直线 上有一定点
上有一定点 ,曲线
,曲线 与
与 交于M,N两点,求
交于M,N两点,求 的值.
的值.
(3)选修4-5:不等式选讲
已知 为实数,且
为实数,且
(Ⅰ)求证:
(Ⅱ)求实数m的取值范围.
查看习题详情和答案>>
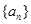 、
、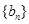 满足
满足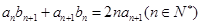 .
.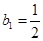 时,求数列
时,求数列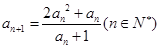 ,
,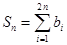 ,求证:
,求证: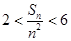 .
. 、
、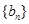 满足
满足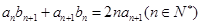 .
. 时,求数列
时,求数列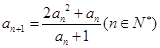 ,
,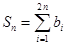 ,求证:
,求证: .
.