摘要：设集合.P是坐标平面上的点..． (1)P可以表示多少个平面上的不同的点? (2)P可以表示多少个第二象限内的点? (3)P可以表示多少个不在直线y=x上的点? 高三数学教学案 第十章 排列.组合.二项式定理 第二课时 排列与组合(一) 考纲摘录 理解排列与组合的意义.掌握排列数与组合数的计算公式.掌握组合数的两个性质. 并能运用它们解决一些简单的应用问题． 知识概要
网址：http://m.1010jiajiao.com/timu3_id_511689[举报]
在平面直角坐标系中，已知O为坐标原点，点A的坐标为（a，b），点B的坐标为（cosωx，sinωx），其中a2+b2≠0且ω＞0．设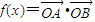
．
（1）若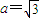
，b=1，ω=2，求方程f（x）=1在区间[0，2π]内的解集；
（2）若点A是过点（-1，1）且法向量为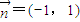
的直线l上的动点．当x∈R时，设函数f（x）的值域为集合M，不等式x2+mx＜0的解集为集合P．若P⊆M恒成立，求实数m的最大值；
（3）根据本题条件我们可以知道，函数f（x）的性质取决于变量a、b和ω的值．当x∈R时，试写出一个条件，使得函数f（x）满足“图象关于点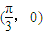
对称，且在
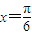处f（x）取得最小值”．
查看习题详情和答案>>
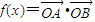．（1）若
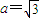，b=1，ω=2，求方程f（x）=1在区间[0，2π]内的解集；（2）若点A是过点（-1，1）且法向量为
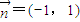的直线l上的动点．当x∈R时，设函数f（x）的值域为集合M，不等式x2+mx＜0的解集为集合P．若P⊆M恒成立，求实数m的最大值；（3）根据本题条件我们可以知道，函数f（x）的性质取决于变量a、b和ω的值．当x∈R时，试写出一个条件，使得函数f（x）满足“图象关于点
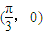对称，且在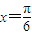处f（x）取得最小值”．查看习题详情和答案>>
设集合M={-3，-2，-1，0，1，2}，P(a,b)是坐标平面上的点，a、b∈M.
（1）P(a,b)可以表示多少个平面上的不同的点？
（2）P(a,b)可以表示多少个第二象限内的点？
（3）P(a,b）可以表示多少个不在直线y=x上的点？
查看习题详情和答案>>设集合M＝{－3，－2，－1，0，1，2}，P(a，b)是坐标平面上的点，a、b∈M，
(1)P可以表示平面上的多少个不同的点？
(2)P可以表示多少个第二象限内的点？
(3)P可以表示多少个不在直线y＝x上的点？
设函数的集合P={f(x)=log2(x+a)+b|a=-
，0，
，1；b=-1，0，1}，
平面上点的集合Q={(x，y)|x=-
，0，
，1；y=-1，0，1}，
则在同一直角坐标系中，P中函数f（x）的图象恰好经过Q中两个点的函数的个数是（ ）
| 1 |
| 2 |
| 1 |
| 2 |
平面上点的集合Q={(x，y)|x=-
| 1 |
| 2 |
| 1 |
| 2 |
则在同一直角坐标系中，P中函数f（x）的图象恰好经过Q中两个点的函数的个数是（ ）
| A、4 | B、6 | C、8 | D、10 |
在平面直角坐标系中，已知O为坐标原点，点A的坐标为（a，b），点B的坐标为（cosωx，sinωx），其中a2+b2≠0且ω＞0．设f(x)=
•
．
（1）若a=
，b=1，ω=2，求方程f（x）=1在区间[0，2π]内的解集；
（2）若点A是过点（-1，1）且法向量为
=(-1，1)的直线l上的动点．当x∈R时，设函数f（x）的值域为集合M，不等式x2+mx＜0的解集为集合P．若P⊆M恒成立，求实数m的最大值；
（3）根据本题条件我们可以知道，函数f（x）的性质取决于变量a、b和ω的值．当x∈R时，试写出一个条件，使得函数f（x）满足“图象关于点(
，0)对称，且在x=
处f（x）取得最小值”．
查看习题详情和答案>>
| OA |
| OB |
（1）若a=
| 3 |
（2）若点A是过点（-1，1）且法向量为
| n |
（3）根据本题条件我们可以知道，函数f（x）的性质取决于变量a、b和ω的值．当x∈R时，试写出一个条件，使得函数f（x）满足“图象关于点(
| π |
| 3 |
| π |
| 6 |