摘要:13.①已知a,b∈R+.n∈N+.试比较(a+b)(an+bn)与2(an+1+bn+1)的大小. ②已知x,y,z∈R+.试比较x2xy2yz2z与xy+zyz+xzx+y的大小.
网址:http://m.1010jiajiao.com/timu3_id_511556[举报]
已知函数f(x)=ax4+bx3+cx2+dx+e(a,b,c,d,∈R)是定义在R上的奇函数,且f(x)在x=
处取得极小值-
.设f′(x)表示f(x)的导函数,定义数列{an}满足:an=f′(
)+2(n∈N*)).
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)对任意m,n∈N*,若m≤n,证明:1+
≤(1+
)m<3;
(Ⅲ)(理科)试比较(1+
)m+1与(1+
)m+2的大小.
查看习题详情和答案>>
| 2 |
4
| ||
| 3 |
| n |
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)对任意m,n∈N*,若m≤n,证明:1+
| m |
| an |
| 1 |
| an |
(Ⅲ)(理科)试比较(1+
| 1 |
| an |
| 1 |
| an+1 |
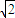 处取得极小值-
处取得极小值-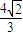 .设f′(x)表示f(x)的导函数,定义数列{an}满足:an=f′(
.设f′(x)表示f(x)的导函数,定义数列{an}满足:an=f′(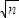 )+2(n∈N*)).
)+2(n∈N*)).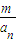 ≤(1+
≤(1+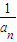 )m<3;
)m<3;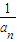 )m+1与(1+
)m+1与(1+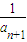 )m+2的大小.
)m+2的大小.