摘要:解:(Ⅰ).令.依条件(3)可得f (0+0)≥f (0)+f (0),即f (0)≤0 又由条件(1)得f (0) ≥0.则f (0)= 0 (Ⅱ)任取0≤≤1.可知. 则. 即≥0.故于是当0≤x≤1时.有f (x) ≤f (1) =1,因此.当x=1时.f (x)有最大值1 (Ⅲ)证明:当时.f (x) ≤1<2x 当时.f (2x) ≥f (x)+f (x)=2f (x).∴ (Ⅳ)证明:当时.f (x) ≤1≤2x 当时.f (2x) ≥f (x)+f (x)=2 f(x).∴. 显然.当时.··成立 假设当时.有成立.其中k=1,2,- 那么当时. ···· 可知对于 .总有.其中n∈N* 此时.故时.有f (x)<2x
网址:http://m.1010jiajiao.com/timu3_id_511477[举报]
解:因为有负根,所以![]() 在y轴左侧有交点,因此
在y轴左侧有交点,因此![]()
解:因为函数没有零点,所以方程![]() 无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
13.证明:(1)令x=y=1,由已知可得f(1)=f(1×1)=f(1)f(1),所以f(1)=1或f(1)=0
若f(1)=0,f(0)=f(1×0)=f(1)f(0)=0,所以f(1)=f(0)与已知条件“![]() ”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
(2)因为f(1)=f[(-1)×(-1)]=f2(-1)=,所以f(-1)=±1,但若f(-1)=1,则f(-1)=f(1)与已知矛盾所以f(-1)不能等于1,只能等于-1。所以任x∈R,f(-x)=f(-1)f(x)=-f(x),因此函数是奇函数
数字1,2,3,4恰好排成一排,如果数字i(i=1,2,3,4)恰好出现在第i个位置上则称有一个巧合,求巧合数![]() 的分布列。
的分布列。
在△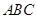 中,∠
中,∠ ,∠
,∠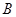 ,∠
,∠ 的对边分别是
的对边分别是 ,且
,且
 .
.
(1)求∠ 的大小;(2)若
的大小;(2)若 ,
, ,求
,求 和
和 的值.
的值.
【解析】第一问利用余弦定理得到
 第二问
第二问
(2) 由条件可得 
将  代入 得 bc=2
代入 得 bc=2
解得 b=1,c=2 或 b=2,c=1 .
查看习题详情和答案>>
14、(1+x)n=Cn0+Cn1x+Cn2x2+…+Cnnxn(x∈N*)(1+x)n=C,上式两边对x求导后令x=1,可得结论:Cn1+2Cn2+…+rCnr+nCnn=n•2n-1,利用上述解题思路,可得到许多结论.试问:Cn0+2Cn1+3Cn2+…+(r+1)Cnr+…+(n+1)Cnn=
查看习题详情和答案>>
(n+2)2n-1
.