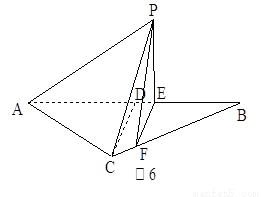摘要: 如图6所示.等腰△ABC的底边AB=6,高CD=3.点B是线段BD上异于点B.D的动点.点F在BC边上.且EF⊥AB.现沿EF将△BEF折起到△PEF的位置.使PE⊥AE.记 BE=x.V(x)表示四棱锥P-ACFE的体积. (1)求V(x)的表达式, (2)当x为何值时.V(x)取得最大值? (3)当V(x)取得最大值时.求异面直线AC与PF所成角的余弦值
网址:http://m.1010jiajiao.com/timu3_id_511073[举报]
(本小题满分14分)
一个几何体的三视图如右图所示,其中正视图和侧视图是腰长为6的两个全等的等腰直角三角形.
(Ⅰ)请画出该几何体的直观图,并求出它的体积;
(Ⅱ)用多少个这样的几何体可以拼成一个棱长为6的正方体ABCD—A1B1C1D1? 如何组拼?试证明你的结论;
(Ⅲ)在(Ⅱ)的情形下,设正方体ABCD—A1B1C1D1的棱CC1的中点为E, 求平面AB1E与平面ABC所成二面角的余弦值。

查看习题详情和答案>>
.(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
如图所示的自动通风设施.该设施的下部 是等腰梯形,其中
是等腰梯形,其中 米,梯形的高为
米,梯形的高为 米,
米, 米,上部
米,上部 是个半圆,固定点
是个半圆,固定点 为
为 的中点.△
的中点.△ 是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),
是由电脑控制其形状变化的三角通风窗(阴影部分均不通风), 是可以沿设施边框上下滑动且始终保持和
是可以沿设施边框上下滑动且始终保持和 平行的伸缩横杆.
平行的伸缩横杆.
(1)设 与
与 之间的距离为
之间的距离为 米,试将三角通风窗
米,试将三角通风窗 的通风面积
的通风面积 (平方米)表示成关于
(平方米)表示成关于 的函数
的函数 ;
;
(2)当 与
与 之间的距离为多少米时,三角通风窗
之间的距离为多少米时,三角通风窗 的通风面积最大?并求出这个最大面积。
的通风面积最大?并求出这个最大面积。

查看习题详情和答案>>
.(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
如图所示的自动通风设施.该设施的下部 是等腰梯形,其中
是等腰梯形,其中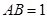 米,梯形的高为
米,梯形的高为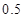 米,
米, 米,上部
米,上部 是个半圆,固定点
是个半圆,固定点 为
为 的中点.△
的中点.△ 是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),
是由电脑控制其形状变化的三角通风窗(阴影部分均不通风), 是可以沿设施边框上下滑动且始终保持和
是可以沿设施边框上下滑动且始终保持和 平行的伸缩横杆.
平行的伸缩横杆.
(1)设 与
与 之间的距离为
之间的距离为 米,试将三角通风窗
米,试将三角通风窗 的通风面积
的通风面积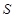 (平方米)表示成关于
(平方米)表示成关于 的函数
的函数 ;
;
(2)当 与
与 之间的距离为多少米时,三角通风窗
之间的距离为多少米时,三角通风窗 的通风面积最大?并求出这个最大面积。
的通风面积最大?并求出这个最大面积。

如图所示的自动通风设施.该设施的下部
 是等腰梯形,其中
是等腰梯形,其中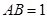 米,梯形的高为
米,梯形的高为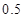 米,
米, 米,上部
米,上部 是个半圆,固定点
是个半圆,固定点 为
为 的中点.△
的中点.△ 是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),
是由电脑控制其形状变化的三角通风窗(阴影部分均不通风), 是可以沿设施边框上下滑动且始终保持和
是可以沿设施边框上下滑动且始终保持和 平行的伸缩横杆.
平行的伸缩横杆.(1)设
 与
与 之间的距离为
之间的距离为 米,试将三角通风窗
米,试将三角通风窗 的通风面积
的通风面积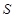 (平方米)表示成关于
(平方米)表示成关于 的函数
的函数 ;
;(2)当
 与
与 之间的距离为多少米时,三角通风窗
之间的距离为多少米时,三角通风窗 的通风面积最大?并求出这个最大面积。
的通风面积最大?并求出这个最大面积。
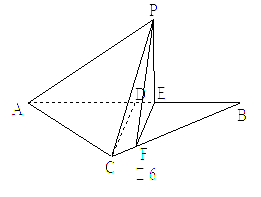 记BE=x,V(x)表示四棱锥P-ACFE的体积。
记BE=x,V(x)表示四棱锥P-ACFE的体积。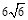 ,高CD=3.点E是线段BD上异于B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.
,高CD=3.点E是线段BD上异于B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.