摘要:当正数k∈ 时.函数f(x)=kx3+3(k-1)x2-k2+1在(0.4)上是减函数. 例题讲解 例1:已知函数f(x)=-x3+ax2 +b 上单调递增.求a的取值范围 (2)当a>0时.若函数满足y极小值=1.y极大值=.试求y=f(x)的解析式 图象上任意一点处的切线倾斜角为θ.求0≤θ≤时.a的取值范围 例2:设抛物线C1:y=x2-2x+2与C2:y=-x2+ax+b在它们同一个交点处的切线互相垂直. (1)求a.b之间的关系 (2)若a>0.b>0.求ab的最大值 例3:f(x)=ax3+bx2+cx的图象关于原点对称.A,B分别为函数的极大值点和极小值点.且|AB|=2.f= β-α. (1) 求b的值 的解析式 与x2-y2=0的交点,并根据图形结构特点找出区间E=[m.n]使E={f(x)|x∈E} 课后作业 班级 学号 姓名
网址:http://m.1010jiajiao.com/timu3_id_510851[举报]
设函数f(x)在(-∞,+∞)内有定义,对于给定的正数K,定义函数:fK(x)=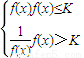 ,取函数f(x)=a11(a>1).当K=
,取函数f(x)=a11(a>1).当K=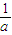 时,函数f(x)值域是( )
时,函数f(x)值域是( )
A.[0,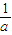 ]∪[1,a)
]∪[1,a)
B.(0,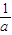 ]∪[1,a]
]∪[1,a]
C.(0,1]∪[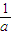 ,a)
,a)
D.(0, ]∪[1,a)
]∪[1,a)
查看习题详情和答案>>
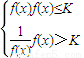 ,取函数f(x)=a11(a>1).当K=
,取函数f(x)=a11(a>1).当K=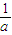 时,函数f(x)值域是( )
时,函数f(x)值域是( )A.[0,
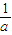 ]∪[1,a)
]∪[1,a)B.(0,
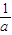 ]∪[1,a]
]∪[1,a]C.(0,1]∪[
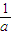 ,a)
,a)D.(0,
 ]∪[1,a)
]∪[1,a)查看习题详情和答案>>
设函数f(x)在(-∞,+∞)内有定义,对于给定的正数K,定义函数:fK(x)= ,取函数f(x)=a11(a>1).当K=
,取函数f(x)=a11(a>1).当K= 时,函数f(x)值域是
时,函数f(x)值域是
- A.[0,
 ]∪[1,a)
]∪[1,a) - B.(0,
 ]∪[1,a]
]∪[1,a] - C.(0,1]∪[
 ,a)
,a) - D.(0,
 ]∪[1,a)
]∪[1,a)
若函数f(x)=ax3-bx+4,当x=2时,函数f(x)有极值-
.
(1)求函数的解析式;
(2)求函数的极值;
(3)若关于x的方程f(x)=k有三个零点,求实数k的取值范围.
查看习题详情和答案>>
| 4 | 3 |
(1)求函数的解析式;
(2)求函数的极值;
(3)若关于x的方程f(x)=k有三个零点,求实数k的取值范围.