摘要：5．定义在满足 ① 任意x.y∈＝f ().②x∈时. 有f(x) >0 1) 判定f上的奇偶性.并说明理由 2) 判定f上的单调性.并给出证明 3) 求证:f ()＝f ()-f () 或f ()+f ()+-+f ()> f () (n∈N*) 解:1) 定义在满足任意x.y∈ 都有f＝f (),则当y=0时, f f(0)=0 当-x=y时, f f上的奇函数 2) 设0>x1>x2>-1 f(x1)-f(x2)= f(x1)+ f(-x2)= 0>x1>x2>-1 ,x∈时. 有f(x) >0,1-x1 x2>0, x1-x2>0 >0 即f上单调递增. 3) f ()=f() =f( )=f() =f()-f() f ()+f ()+-+f () =f()-f()+f()-f()+f()+-+f()-f() = f() -f()=f()+f(-) x∈ >0 f(-)>0, f()+f(-)>f() 即f ()+f ()+-+f ()> f () 1)
网址：http://m.1010jiajiao.com/timu3_id_510467[举报]
定义在(-1，1)上的函数f(x)满足:
①对任意x、y∈(-1,1)，都有f(x)+f(y)= 
.?
②当x∈(-1，0)时，有f(x)＞0.
(1)求证:函数f(x)是奇函数；
(2)判断f(x)在(-1，1)上的单调性，并加以证明；
(3)设-1＜a＜1，试求不等式f(a)+f(
)＞0的解.
定义在(-1，1)上的函数f(x)满足：对任意x，y∈(-1，1)，都有f(x)+f(y)=f(
).
).(1)求证：函数f(x)是奇函数；
(2)若当x∈(-1，0)时，有f(x)＞0，求证：f(x)在(-1，1)上是减函数.
查看习题详情和答案>>定义在(0，＋∞)上的函数f(x)满足对任意m＞0，n∈R有f(mn)＝nf(m)，且当0＜x＜1时f(x)＜0
(Ⅰ)求f(x)；
(Ⅱ)证明：当x＞1时，f(x)＞0
(Ⅲ)证明：函数f(x)在(0，＋∞)上递增．
的值；(用含p的式子表示)；
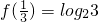，且对于任意的x∈[-1，1]都有f（x+y）=f（x）+f（y）．