摘要:函数的定义及通性,
网址:http://m.1010jiajiao.com/timu3_id_510415[举报]
函数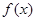 的定义域为
的定义域为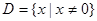 ,且满足对于任意
,且满足对于任意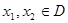 ,有
,有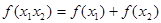 .
.
⑴求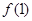 的值;
的值;
⑵判断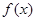 的奇偶性并证明;
的奇偶性并证明;
⑶如果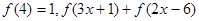 ≤
≤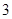 ,且
,且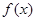 在
在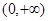 上是增函数,求
上是增函数,求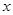 的取值范围.
的取值范围.
【解析】(Ⅰ) 通过赋值法,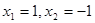 ,求出f(1)0;
,求出f(1)0;
(Ⅱ) 说明函数f(x)的奇偶性,通过令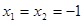 ,得
,得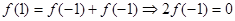 .令
.令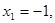
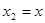 ,得
,得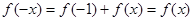 ,推出对于任意的x∈R,恒有f(-x)=f(x),f(x)为偶函数.
,推出对于任意的x∈R,恒有f(-x)=f(x),f(x)为偶函数.
(Ⅲ) 推出函数的周期,根据函数在[-2,2]的图象以及函数的周期性,即可求满足f(2x-1)≥12的实数x的集合.
查看习题详情和答案>>
设函数f(x)的定义域为R,当x<0时f(x)>1,且对任意的实数x,y∈R,有![]()
(Ⅰ)求f(0),判断并证明函数f(x)的单调性;
(Ⅱ)数列![]() 满足
满足![]() ,且
,且![]() ,数列
,数列![]() 满足
满足![]() w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m ![]()
①求数列![]() 通项公式。
通项公式。
②求数列![]() 的前n项和Tn的最小值及相应的n的值.
的前n项和Tn的最小值及相应的n的值.
已知f(x)是定义在R上的不恒为零的函数,且对于任意的a,b∈R都满足:f(ab)=af(b)+bf(a).
(1)求f(0)及f(1)的值;
(2)判断的奇偶性,并证明你的结论;
(3)若f(2)=2,un=
(n∈N*),求证数列{un}是等差数列,并求{un}的通项公式.
查看习题详情和答案>>
(1)求f(0)及f(1)的值;
(2)判断的奇偶性,并证明你的结论;
(3)若f(2)=2,un=
| f(2n) | 2n |
 ,求证数列{un}是等差数列,并求{un}的通项公式.
,求证数列{un}是等差数列,并求{un}的通项公式.