摘要:直线是平面几何的基本图形.它与方程中的二元一次方程Ax+By+C=0(A2+B2≠0)一一对应. 从几何条件看.已知直线上一点及直线方向与已知直线上两点均可确定直线,从对应方程看.直线方程两种典型形式:点斜式.两点式.因此求直线方程.常用待定系数法.即根据题意.选择方程的适当形式,由已知条件.列关于参数的方程(组). 当点P(x0.y0)在直线Ax+By+C=0上时.其坐标满足方程Ax0+By0+C=0,当P不在直线Ax+By+C=0上时.Ax0+By0+C≠0.即Ax0+By0+C>0或Ax0+By0+C<0.这就是二元一次不等式的几何意义:二元一次不等式Ax+By+C>0表示直线Ax+By+C=0上方或下方区域.其具体位置的确定常用原点(0.0)代入检验.利用此几何意义.可以解决一类二元函数的最值问题.这就是线性规划的内容. 因直线与二元一次方程Ax+By+C=0(A2+B2≠0)一一对应.即由有序数组确定.因此研究直线与直线之间的位置关系就是考察直线对应的数组间关系. 设直线1:A1x+B1y+C1=0(A12+B12≠0).直线2:A2x+B2y+C2=0(A22+B22≠0) 则:1∥2 1与2相交A1B2≠A2B1 其夹角公式为.其中k1.k2分别表示1及2斜率.当1或2斜率不存在时.画图通过三角形求解.1与2夹角为θ∈(0.] 特例:1⊥2A1A2+B1B2=0(此时不能用夹角公式求解) 利用点P(x0.y0)到直线:Ax+By+C=0的距离公式d=可以求出两平行直线:Ax+By+C1=0.Ax+By+C2=0(C1≠C2)间的距离d=.
网址:http://m.1010jiajiao.com/timu3_id_510380[举报]
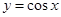 与
与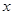 轴、
轴、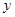 轴、直线
轴、直线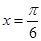 围成的封闭图形的面积为
围成的封闭图形的面积为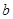 ,若
,若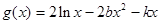 在
在 上单调递减,则实数
上单调递减,则实数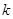 的取值范围是 。
的取值范围是 。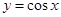 与
与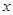 轴、
轴、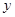 轴、直线
轴、直线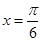 围成的封闭图形的面积为
围成的封闭图形的面积为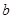 ,若
,若 在
在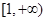 上单调递减,则实数
上单调递减,则实数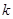 的取值范围是 。
的取值范围是 。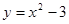 与直线
与直线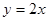 围成的封闭图形的面积是( )
围成的封闭图形的面积是( )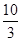
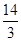
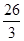
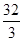
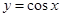 与
与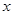 轴、
轴、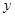 轴、直线
轴、直线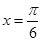 围成的封闭图形的面积为
围成的封闭图形的面积为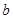 ,若
,若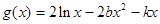 在
在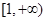 上单调递减,则实数
上单调递减,则实数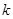 的取值范围是
。
的取值范围是
。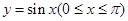 与直线
与直线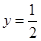 围成的封闭图形的面积是 ( )
围成的封闭图形的面积是 ( )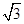 B.
B.
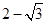 C.
C.
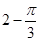 D.
D.