题目内容
阅读下列材料,然后解答问题;对于任意实数x,符号[x]表示“不超过x的最大整数”,在数轴上,当x是整数,[x]是x,当x不是整数时,[x]是x左侧的第一个整数,这个函数叫做“取整函数”,也叫高斯(Gauss)函数,如[-2]=-2、[-1.5]=-2、[2.5]=2 定义函数{x}=x-[x],给出下列四个命题;
①函数[x]的定义域是R,值域为[0,1];
②方程{x}=
| 1 | 2 |
③函数{x}是周期函数;
④函数{x}是增函数.
其中正确命题的序号是
分析:通过举反例,可得①④不正确,通过x=1.5,2.5,3.5,4.5,…时,函数{x}的值都是
,说明②③正确.
| 1 |
| 2 |
解答:解:①不正确,如x=8.8时,[x]=8,显然函数的值域不是[0,1].
②正确,由于函数{x}=x-[x]的值域是[0,1),
当x=1.5,2.5,3.5,4.5,…时,都是此方程{x}=
的解.
由②知,函数{x}是周期函数,故③正确.
④不正确,如x=1.5,2.5,3.5,4.5,…时,函数{x}的值都是
,故不是增函数.
综上,②③正确,
故答案为 ②③.
②正确,由于函数{x}=x-[x]的值域是[0,1),
当x=1.5,2.5,3.5,4.5,…时,都是此方程{x}=
| 1 |
| 2 |
由②知,函数{x}是周期函数,故③正确.
④不正确,如x=1.5,2.5,3.5,4.5,…时,函数{x}的值都是
| 1 |
| 2 |
综上,②③正确,
故答案为 ②③.
点评:本题考查新定义函数 {x}=x-[x]的意义,通过举反例来说明某个命题的正确性,是一种简单有效的方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,问函数g(x)是否存在最大值或最小值?若存在,求出最大值或最小值;若不存在,说明理由.一个同学给出了如下解答:
,问函数g(x)是否存在最大值或最小值?若存在,求出最大值或最小值;若不存在,说明理由.一个同学给出了如下解答: )2+
)2+ ,
, 时,u有最大值,umax=
时,u有最大值,umax= ,显然u没有最小值,
,显然u没有最小值, 时,g(x)有最小值4,没有最大值.
时,g(x)有最小值4,没有最大值. ,请提出此问题的一个结论,例如:求通项an.并给出正确解答.
,请提出此问题的一个结论,例如:求通项an.并给出正确解答.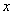 ,符号[
,符号[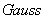 )函数,如[-2]=-2、[-1.5]=-2、[2.5]=2 定义函数{
)函数,如[-2]=-2、[-1.5]=-2、[2.5]=2 定义函数{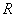 ,值域为[0,1]
,值域为[0,1] 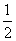 有无数个解;
有无数个解;