摘要:从新教材开始的新高考命题统计看,对向量与三角的考查立足于基础题和中档题.位置一般在选择的前位和解答题的前三个. 04年全国14套试卷每一套解答题的第一题都是有关三角或向量,不是三角求值,就是三角函数,或向量与三角相结合.而小题主要是三角函数图象性质,或是利用诱导公式与倍角公式进行三角变形求值.但新教材与老教材最明显的区别就在于降低了三角变形要求.这在新高考中得到了充分的体现. 如03年江苏卷19题已知函数f(x)=sin(x+)是R上的偶函数,其图象关于点(,0)对称,且在区间[0,]上是单调函数,求和的值 03新课程理17已知函数f Ⅰ.求函数f(x)的最小正周期和最大值 Ⅱ.在给出的坐标系中画出函数y=f(x)在区间[o,]上的图象 已知tan(+)= Ⅰ.求tan值 Ⅱ.求的值 已知,,求的值. 以上考题,都表明了删除繁杂的三角变形,但三角公式还是要熟练的.如江苏17题若不知半角的切公式,应用常规的切化弦亦可以.从江苏03年的第19题可知对三角函数的要求却远远超出考纲中的了解. 向量是新增内容,从新高考命题思路看,主要是把向量作为工具与三角或解几立几相结合进行考查.或在小题中对向量的概念基本运算进行考查.命题的重点在向量的坐标式与向量的几何形式与向量的矢量式三种. 如去年如图在Rt△ABC中, 已知BC=a,若长为2a的线段PQ以点A为中点,问与的夹角取何值时, 的值最大并求出这个最大值. 平面向量a,b中,已知a=,|b|=1,且a•b=5则向量b. 这些考题说明对向量的要求围绕考纲要求设计考题.但向量的三种形式进行了全方位的考查.因此对向量的复习要围绕考纲进行设计试题. 2004年全理 2004全新理 2004天津 2004江苏 2003年新江苏 选择题 3 5.10.11 3.12 2 填空题 16 解答题 17三角变形求值 17解三角形 17求值22向量与解几 17三角求值
网址:http://m.1010jiajiao.com/timu3_id_510013[举报]
已知某企业的原有产品每年投入x万元,可获得的年利润表示为函数:P(x)=-
(x-30)2+20(万元).现准备开发一个回报率高,科技含量高的新产品从“十一五”计划(此计划历时5年)的第一年开始,用两年的时间完成.这两年,每年从100万元的生产准备金中拿出80万元投入新产品的开发,从第三年开始这100万元就可全部用于新旧两种产品的生产投入.经预测,新产品每年投入x万元,可获得的年利润表示为函数:Q(x)=-
(100-x)2+48(100-x)(万元).
(1)为了解决资金缺口,第一年初向银行贷款1000万元,年利率为5.5%(不计复利),第五年底一次性向银行偿还本息共计多少万元?
(2)从新产品投入生产的第三年开始,从100万元的生产准备金中,新旧两种产品各应投入多少万元,才能使后三年的年利润最大?
(3)从新旧产品的五年最高总利润中拿出70%来,能否还清对银行的欠款?
查看习题详情和答案>>
| 1 |
| 10 |
| 9 |
| 10 |
(1)为了解决资金缺口,第一年初向银行贷款1000万元,年利率为5.5%(不计复利),第五年底一次性向银行偿还本息共计多少万元?
(2)从新产品投入生产的第三年开始,从100万元的生产准备金中,新旧两种产品各应投入多少万元,才能使后三年的年利润最大?
(3)从新旧产品的五年最高总利润中拿出70%来,能否还清对银行的欠款?
已知某企业的原有产品,每年投入x万元,可获得的年利润可表示为函数:P(x)=-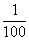 ·(x-30)2+8(万元).现开发一个回报率高、科技含量高的新产品,据预测,新产品每年投入x万元,可获得年利润Q(x)=-
·(x-30)2+8(万元).现开发一个回报率高、科技含量高的新产品,据预测,新产品每年投入x万元,可获得年利润Q(x)=-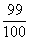 (100-x)2+
(100-x)2+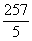 (100-x)(万元).新产品开发从“十五”计划的第一年开始,用两年时间完成.这两年,每年从100万元的生产准备金中,拿出80万元来投入新产品开发.从第三年开始这100万元全部用于新旧两种产品的生产投入.
(100-x)(万元).新产品开发从“十五”计划的第一年开始,用两年时间完成.这两年,每年从100万元的生产准备金中,拿出80万元来投入新产品开发.从第三年开始这100万元全部用于新旧两种产品的生产投入.
(1)为了解决资金缺口,第一年初向银行贷款1 000万元,利率为5.5%(不计复利),第五年底一次性应向银行偿还本息共计多少万元?
(2)从新产品投产的第三年开始,从100万元的生产准备金中,新旧两种产品各应投入多少万元,才能使年利润最大?
(3)从新旧产品的五年总利润中最高拿出70%来,能否还清对银行的欠款?
查看习题详情和答案>>(文)某企业原有产品每年投入x万元,所获年利润为![]() (万元),对开发的新产品,每年投入x万元,所获年利润为
(万元),对开发的新产品,每年投入x万元,所获年利润为![]()
![]() (万元),新产品开发用两年时间完成,这两年,每年从100万元生产准备资金中拿出80万元投入新产品开发,从第三年开始这100万元可随意分配且全部用于新旧产品的生产投入.为解决资金缺口,第一年初向银行贷款1000万元,年利率5.5%(不计复利,即先一年利息不计入下一年本金).(1)第五年底一次性向银行还本息多少万元?(2)从新产品开发的第三年起,新旧产品各投入多少万元年利润最大,最大利润是多少?(3)从新旧产品生产五年的最高利润总和中拿出70%来能否还清贷款?
(万元),新产品开发用两年时间完成,这两年,每年从100万元生产准备资金中拿出80万元投入新产品开发,从第三年开始这100万元可随意分配且全部用于新旧产品的生产投入.为解决资金缺口,第一年初向银行贷款1000万元,年利率5.5%(不计复利,即先一年利息不计入下一年本金).(1)第五年底一次性向银行还本息多少万元?(2)从新产品开发的第三年起,新旧产品各投入多少万元年利润最大,最大利润是多少?(3)从新旧产品生产五年的最高利润总和中拿出70%来能否还清贷款?
已知某企业的原有产品每年投入x万元,可获得的年利润表示为函数: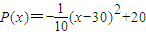 (万元).现准备开发一个回报率高,科技含量高的新产品从“十一五”计划(此计划历时5年)的第一年开始,用两年的时间完成.这两年,每年从100万元的生产准备金中拿出80万元投入新产品的开发,从第三年开始这100万元就可全部用于新旧两种产品的生产投入.经预测,新产品每年投入x万元,可获得的年利润表示为函数:
(万元).现准备开发一个回报率高,科技含量高的新产品从“十一五”计划(此计划历时5年)的第一年开始,用两年的时间完成.这两年,每年从100万元的生产准备金中拿出80万元投入新产品的开发,从第三年开始这100万元就可全部用于新旧两种产品的生产投入.经预测,新产品每年投入x万元,可获得的年利润表示为函数: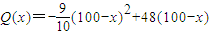 (万元).
(万元).
(1)为了解决资金缺口,第一年初向银行贷款1000万元,年利率为5.5%(不计复利),第五年底一次性向银行偿还本息共计多少万元?
(2)从新产品投入生产的第三年开始,从100万元的生产准备金中,新旧两种产品各应投入多少万元,才能使后三年的年利润最大?
(3)从新旧产品的五年最高总利润中拿出70%来,能否还清对银行的欠款?
查看习题详情和答案>>
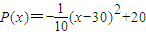 (万元).现准备开发一个回报率高,科技含量高的新产品从“十一五”计划(此计划历时5年)的第一年开始,用两年的时间完成.这两年,每年从100万元的生产准备金中拿出80万元投入新产品的开发,从第三年开始这100万元就可全部用于新旧两种产品的生产投入.经预测,新产品每年投入x万元,可获得的年利润表示为函数:
(万元).现准备开发一个回报率高,科技含量高的新产品从“十一五”计划(此计划历时5年)的第一年开始,用两年的时间完成.这两年,每年从100万元的生产准备金中拿出80万元投入新产品的开发,从第三年开始这100万元就可全部用于新旧两种产品的生产投入.经预测,新产品每年投入x万元,可获得的年利润表示为函数: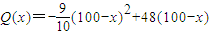 (万元).
(万元).(1)为了解决资金缺口,第一年初向银行贷款1000万元,年利率为5.5%(不计复利),第五年底一次性向银行偿还本息共计多少万元?
(2)从新产品投入生产的第三年开始,从100万元的生产准备金中,新旧两种产品各应投入多少万元,才能使后三年的年利润最大?
(3)从新旧产品的五年最高总利润中拿出70%来,能否还清对银行的欠款?
查看习题详情和答案>>
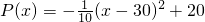 (万元).现准备开发一个回报率高,科技含量高的新产品从“十一五”计划(此计划历时5年)的第一年开始,用两年的时间完成.这两年,每年从100万元的生产准备金中拿出80万元投入新产品的开发,从第三年开始这100万元就可全部用于新旧两种产品的生产投入.经预测,新产品每年投入x万元,可获得的年利润表示为函数:
(万元).现准备开发一个回报率高,科技含量高的新产品从“十一五”计划(此计划历时5年)的第一年开始,用两年的时间完成.这两年,每年从100万元的生产准备金中拿出80万元投入新产品的开发,从第三年开始这100万元就可全部用于新旧两种产品的生产投入.经预测,新产品每年投入x万元,可获得的年利润表示为函数: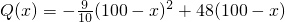 (万元).
(万元).