摘要：如图已知四棱锥P-ABCD.PA⊥平面ABCD.底面ABCD为直角梯形.∠A=90°且AB//CD.AB=CD. (1)点F在线段PC上运动.且设为何值时.BF//平面PAD?并证明你的结论, (2)二面角F-CD-B为45°.求二面角B-PC-D的大小, 的条件下.若AD=2.CD=3.求点A到平面PBC的距离. 解答:(1)当 证明:取PD中点E.则EF//CD.且 ∴四边形ABFE为平行四边形. ∴BF//AE. 又AE平面PAD ∴BF//平面PAD (2)平面ABCD.即是二面角的平 面角 为等腰直角三角形. 平面PCD 又BF//AE.平面PCD. 平面PBC. ∴平面PCD⊥平面PBC.即二面角B-PC-D的大小为90°. (3)在平面PCD内作EH⊥PC于点H.由平面PCD⊥平面PBC且平面PCD 平面PBC=PC知:EH⊥平面PBC. 在. 在代入得: 即点E到平面PBC的距离为 又点A到平面PBC的距离为
网址：http://m.1010jiajiao.com/timu3_id_509535[举报]
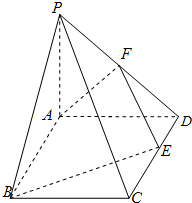如图已知四棱锥P-ABCD中，PA⊥面ABCD，底面ABCD是矩形，AB=| 3 |
（Ⅰ）当点E为CD的中点时，求证EF∥平面PAC，
（Ⅱ）求证：PE⊥AF．
（Ⅲ）在线段CD上是否存在点E，使得直线EF与底面ABCD所成的角为30°，若存在，求出DE的长度，若不存在，请说明理由．
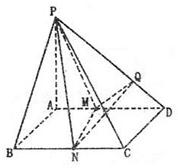已知四棱锥P-ABCD（如图），底面是边长为2的正方形，侧棱PA⊥底面ABCD，M、N分别为AD、BC的中点，MQ⊥PD于Q．（1）求证：平面PMN⊥平面PAD；
（2）PA=2，求PM与平面PCD所成角的正弦值；
（3）求二面角P-MN-Q的余弦值． 查看习题详情和答案>>
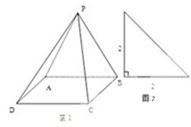已知四棱锥P-ABCD的直观图（如图1）及左视图（如图2），底面ABCD是边长为2的正方形，平面PAB⊥平面ABCD，PA=PB．（Ⅰ）求证：AD⊥PB；
（Ⅱ）求异面直线PD与AB所成角的余弦值；
（Ⅲ）求平面PAB与平面PCD所成锐二面角的大小． 查看习题详情和答案>>
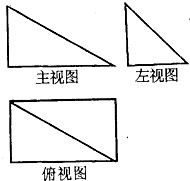已知四棱锥P-ABCD的三视图如右图，该棱锥中，PA=AB=1，PD与平面ABCD所成角是30°，点F是PB的中点，点E在棱BC上移动．
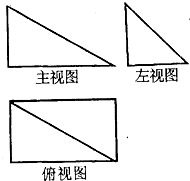已知四棱锥P-ABCD的三视图如右图．该棱锥中，PA=AB=1，PD与平面ABCD所成角是30°，点F是PB的中点，点E在棱BC上移动．