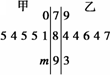
摘要：解:(I)a2＝a1+=a+.a3=a2=a+, (II)因为 a4=a3+=a+, 所以a5=a4=a+, 所以b1=a1-=a-, b2=a3-= (a-), b3=a5-= (a-), 猜想:{bn}是公比为的等比数列. 证明如下:因为bn+1＝a2n+1-=a2n-= (a2n-1-)=bn, (n∈N*) 所以{bn}是首项为a-, 公比为的等比数列· (III).
网址：http://m.1010jiajiao.com/timu3_id_509334[举报]
（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分6分，
第3小题满分8分．
如果数列
同时满足：（1）各项均为正数，（2）存在常数k, 对任意
都成立，那么，这样的数列我们称之为“类等比数列” .由此各项均为正数的等比数列必定是“类等比数列” .问：
（1）若数列为“类等比数列”，且k＝(a2－a1)2，求证：a1、a2、a3成等差数列；
（2）若数列为“类等比数列”，且k＝
， a2、a4、a5成等差数列，求的值；
（3）若数列为“类等比数列”，且a1＝a，a2＝b(a、b为常数)，是否存在常数λ，使得
对任意
都成立？若存在，求出λ；若不存在，说明理由．
第3小题满分8分．
如果数列
同时满足：（1）各项均为正数，（2）存在常数k, 对任意都成立，那么，这样的数列我们称之为“类等比数列” .由此各项均为正数的等比数列必定是“类等比数列” .问：（1）若数列
为“类等比数列”，且k＝(a2－a1)2，求证：a1、a2、a3成等差数列；（2）若数列
为“类等比数列”，且k＝， a2、a4、a5成等差数列，求的值；（3）若数列
为“类等比数列”，且a1＝a，a2＝b(a、b为常数)，是否存在常数λ，使得对任意都成立？若存在，求出λ；若不存在，说明理由．如图是歌手大奖赛中，七位评委为甲、乙两名选手打出的分数的茎叶图(其中m为数字0～9中的一个)，去掉一个最高分和一个最低分后，甲、乙两名选手得分的平均数分别为a1，a2，则有
[ ]
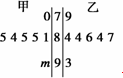
A．a1＞a2
B．a2＝a1
C．a2＞a1
D．a1、a2的大小不确定
