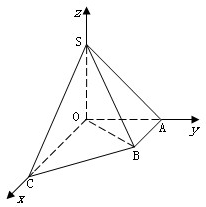
摘要:22.如图直角梯形OABC中.∠COA=∠OAB=.OC=2.OA=AB=1.SO⊥平面OABC.SO=1.以OC.OA.OS分别为x轴.y轴.z轴建立直角坐标系O-xyz. ⑴求的大小, ⑵设 ① ②OA与平面SBC的夹角, ③O到平面SBC的距离. ⑶设 ① . ②异面直线SC.OB的距离为 . 高三单元试题之十:空间向量参考答案
网址:http://m.1010jiajiao.com/timu3_id_509128[举报]
 如图直角梯形OABC中,∠COA=∠OAB=
如图直角梯形OABC中,∠COA=∠OAB=| π |
| 2 |
(1)求
| SC |
| OB |
(2)设
| n |
| n |
①
| n |
②OA与平面SBC的夹角β(用反三角函数表示);
③O到平面SBC的距离.
(3)设
| k |
| k |
| SC |
| k |
| OB |
①
| k |
②异面直线SC、OB的距离为
如图直角梯形OABC中,![]() ,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
(Ⅰ)求![]() 的大小(用反三角函数表示);
的大小(用反三角函数表示);
(Ⅱ)设![]()
①![]()
②OA与平面SBC的夹角![]() (用反三角函数表示);
(用反三角函数表示);
③O到平面SBC的距离.
(Ⅲ)设![]()
①![]() .
.
②异面直线SC、OB的距离为 .
(注:(Ⅲ)只要求写出答案).

.如图直角梯形OABC中,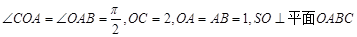 ,
,
SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
(Ⅰ)求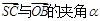 的余弦值;
的余弦值;
(Ⅱ)设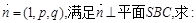
①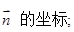
②设OA与平面SBC所成的角为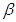 ,求
,求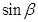 。
。

查看习题详情和答案>>
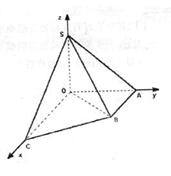
 ,OC=2,OA=AB=1,SO⊥平面OABC,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
,OC=2,OA=AB=1,SO⊥平面OABC,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz. 的大小(用反三角函数表示);
的大小(用反三角函数表示); =(1,p,q),满足
=(1,p,q),满足 ⊥平面SBC,求:
⊥平面SBC,求: 的坐标;
的坐标;
 的坐标为______.
的坐标为______.