摘要：12．设f(x).g(x)分别是定义在R上的奇函数和偶函数.当x <0时.f ′(x)g(x)+f(x)g′(x)>0. 且g(-3)＝0.则不等式f(x)g(x)<0的解集是 ( ) A． B． C． D．
网址：http://m.1010jiajiao.com/timu3_id_509074[举报]
设f(x)，g(x)分别是定义在R上的奇函数和偶函数，当x<0时，
，且
，则不等式
的解集是( ）
A．(－3，0)∪(3，+∞) B．(－3，0)∪(0，3)
C．(－∞，－3)∪(3，+∞) D．(－∞，－3)∪(0，3)
查看习题详情和答案>>
设f(x)，g(x)分别是定义在R上的奇函数和偶函数，当x<0时，
，且
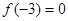，则不等式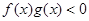
的解集是( ）
A．(－3，0)∪(3，+∞) B．(－3，0)∪(0，3)
C．(－∞，－3)∪(3，+∞) D．(－∞，－3)∪(0，3)
查看习题详情和答案>>
设f(x)，g(x)分别是定义在R上的奇函数和偶函数．当x<0时，f′(x)g(x)＋f(x)g′(x)>0，且g(－3)＝0，则不等式f(x)g(x)<0的解集是( )
A．(－3,0)∪(3，＋∞) B．(－3,0)∪(0,3)
C．(－∞，－3)∪(3，＋∞) D．(－∞，－3)∪(0,3)
查看习题详情和答案>>