摘要:18.(1)依题意.随机变量的取值是2.3.4.5.6.----2分 因为P(=2)=,P(=3)=. P(=4)=,P(=5)=, P(=6)=,----7分 所以.当=4时.其发生的概率P(=4)=最大.----8分 (Ⅱ)E=.------12分
网址:http://m.1010jiajiao.com/timu3_id_508293[举报]
(本题满分12分)有混在一起质地均匀且粗细相同的长分别为1![]() 、2
、2![]() 、3
、3![]() 的钢管各3根(每根钢管附有不同的编号),现随意抽取4根(假设各钢管被抽取的可能性是均等的),再将抽取的4根首尾相接焊成笔直的一根.
的钢管各3根(每根钢管附有不同的编号),现随意抽取4根(假设各钢管被抽取的可能性是均等的),再将抽取的4根首尾相接焊成笔直的一根.
(1)若用ξ表示新焊成的钢管的长度(焊接误差不计),试求随机变量![]() 的分布列及
的分布列及![]() ;
;
(2)设![]() 的取值从小到大依次为
的取值从小到大依次为![]() 数列
数列![]() 是首项为1,公差为
是首项为1,公差为![]() 的等差数列,设
的等差数列,设![]() ,当
,当![]() 时,求
时,求![]() 的值。
的值。
(本题满分12分)有混在一起质地均匀且粗细相同的长分别为1 、2
、2 、3
、3 的钢管各3根(每根钢管附有不同的编号),现随意抽取4根(假设各钢管被抽取的可能性是均等的),再将抽取的4根首尾相接焊成笔直的一根.
的钢管各3根(每根钢管附有不同的编号),现随意抽取4根(假设各钢管被抽取的可能性是均等的),再将抽取的4根首尾相接焊成笔直的一根.
(1)若用ξ表示新焊成的钢管的长度(焊接误差不计),试求随机变量 的分布列及
的分布列及 ;
;
(2)设 的取值从小到大依次为
的取值从小到大依次为 数列
数列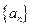 是首项为1,公差为
是首项为1,公差为 的等差数列,设
的等差数列,设 ,当
,当 时,求
时,求 的值。
的值。
 、2
、2 、3
、3 的钢管各3根(每根钢管附有不同的编号),现随意抽取4根(假设各钢管被抽取的可能性是均等的),再将抽取的4根首尾相接焊成笔直的一根.
的钢管各3根(每根钢管附有不同的编号),现随意抽取4根(假设各钢管被抽取的可能性是均等的),再将抽取的4根首尾相接焊成笔直的一根.(1)若用ξ表示新焊成的钢管的长度(焊接误差不计),试求随机变量
 的分布列及
的分布列及 ;
;(2)设
 的取值从小到大依次为
的取值从小到大依次为 数列
数列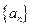 是首项为1,公差为
是首项为1,公差为 的等差数列,设
的等差数列,设 ,当
,当 时,求
时,求 的值。
的值。现有4个人去参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择.为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏.
(Ⅰ)求这4个人中恰有2人去参加甲游戏的概率;
(Ⅱ)求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率;
(Ⅲ)用X,Y分别表示这4个人中去参加甲、乙游戏的人数,记 ,求随机变量
,求随机变量 的分布列与数学期望
的分布列与数学期望 .
.
【解析】依题意,这4个人中,每个人去参加甲游戏的概率为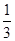 ,去参加乙游戏的概率为
,去参加乙游戏的概率为 .
.
设“这4个人中恰有i人去参加甲游戏”为事件

则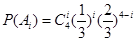 .
.
(1)这4个人中恰有2人去参加甲游戏的概率
(2)设“这4个人中去参加甲游戏的人数大于去参加乙游戏的人数”为事件B,则 .由于
.由于 互斥,故
互斥,故
所以,这个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率为 .
.
(3) 的所有可能取值为0,2,4.由于
的所有可能取值为0,2,4.由于 互斥,
互斥, 互斥,故
互斥,故
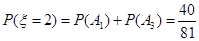

所以 的分布列是
的分布列是
|
|
0 |
2 |
4 |
|
P |
|
|
|
随机变量 的数学期望
的数学期望 .
.
查看习题详情和答案>>


