摘要: 二次函数f(x)满足且f(0)=1. (1) 求f(x)的解析式; (2) 在区间上,y= f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围. 解: =ax2+bx+c.由f=ax2+bx+1. ∵f2+b(x+1)+1-(ax2+bx+1)=2x. 即2ax+a+b=2x,所以,∴f(x)=x2-x+1. (2)由题意得x2-x+1>2x+m在[-1,1]上恒成立.即x2-3x+1-m>0在[-1,1]上恒成立. 设g(x)= x2-3x+1-m,其图象的对称轴为直线x=,所以g(x) 在[-1,1]上递减. 故只需g(1)>0,即12-3×1+1-m>0,解得m<-1.
网址:http://m.1010jiajiao.com/timu3_id_508189[举报]
(本小题满分14分)二次函数f (x) 满足f (x+1)-f (x)=2 x,且f (0)=1.
(1)求f (x)的解析式;
(2)设函数![]() ,若
,若![]() 在R上恒成立,求实数m的范围.
在R上恒成立,求实数m的范围.
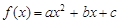 满足:①
满足:①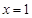 时有极值;②图象过点
时有极值;②图象过点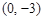 ,且在该点处的切线斜率为
,且在该点处的切线斜率为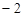 .
.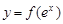 上任意一点的切线的斜率恒大于
上任意一点的切线的斜率恒大于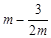 ,求
,求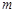 的取值范围;
的取值范围;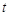 满足什么条件时,函数
满足什么条件时,函数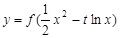 的图象与坐标轴没有公共点?
的图象与坐标轴没有公共点?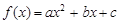 满足:①
满足:①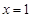 时有极值;②图象过点
时有极值;②图象过点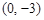 ,且在该点处的切线斜率为
,且在该点处的切线斜率为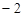 .
.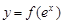 上任意一点的切线的斜率恒大于
上任意一点的切线的斜率恒大于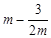 ,求
,求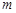 的取值范围;
的取值范围;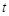 满足什么条件时,函数
满足什么条件时,函数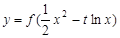 的图象与坐标轴没有公共点?
的图象与坐标轴没有公共点?