摘要:讲解例1 例1 计算.
网址:http://m.1010jiajiao.com/timu3_id_508021[举报]
为讲解信赖区间与信心水平,数学老师请全班40位同学使用老师提供的随机数表模拟投掷均匀铜板16次。模拟的过程如下:随机指定给每位同学随机数表的某一列,该列从左到右有16个数字;如果数字为0,1,2,3,4时,对应投掷铜板得到正面;而数字为5,6,7,8,9时,对应投掷得到反面。某同学拿到的一列数字依序为:
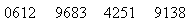
该同学计算铜板出现正面的机率在95%信心水平下的信赖区间:
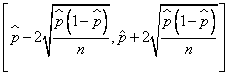 。
。
则该同学所得到的结果中,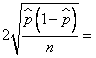 ( )(化为最简根式) 。
( )(化为最简根式) 。
查看习题详情和答案>>
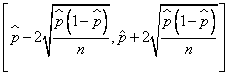 。
。则该同学所得到的结果中,
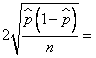 ( )(化为最简根式) 。
( )(化为最简根式) 。有一种树木栽植五年后可成材.在栽植后五年内,年增加20%,如果不砍伐,从第六年到第十年,年增长10%,现有两种砍伐方案:
甲方案:栽植五年后不砍伐,等到十年后砍伐.
乙方案:栽植五年后砍伐重栽,再过五年再砍伐一次.
请计算后回答:十年内哪一个方案可以得到较多的木材?
查看习题详情和答案>>
甲方案:栽植五年后不砍伐,等到十年后砍伐.
乙方案:栽植五年后砍伐重栽,再过五年再砍伐一次.
请计算后回答:十年内哪一个方案可以得到较多的木材?
为了了解某地母亲身高x与女儿身高y的相关关系,随机测得10对母女的身高如下表所示:
计算x与y的相关系数r=0.71,通过查表得r的临界值r0.05=
查看习题详情和答案>>
| 母亲身高x(cm) | 159 | 160 | 160 | 163 | 159 | 154 | 159 | 158 | 159 | 157 |
| 女儿身高y(cm) | 158 | 159 | 160 | 161 | 161 | 155 | 162 | 157 | 162 | 156 |
0.632
0.632
,从而有95%
95%
的把握认为x与y之间具有线性相关关系,因而求回归直线方程是有意义的.通过计算得到回归直线方程为y=35.2+0.78x,当母亲身高每增加1cm时,女儿身高0.78
0.78
,当母亲的身高为161cm时,估计女儿的身高为161cm
161cm
cm.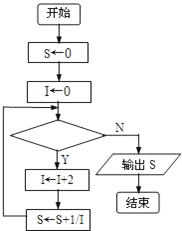 如图给出的是计算
如图给出的是计算