摘要： 已知a＞0.函数.x∈[0.+∞).设x1＞0.记曲线y＝f (x)在点M (x1.f (x1))处的切线为l． (1)求l的方程, (2)设l与x轴交点为(x2.0).证明:①x2≥.②若.则．
网址：http://m.1010jiajiao.com/timu3_id_506007[举报]
（本小题满分12分）
已知m＝(cosωx＋sinωx，
cosωx)，n＝(cosωx－sinωx，2sinωx)，其中ω＞0，若函数f(x)＝m·n，且f(x)的对称中心到f(x)的对称轴的最近距离不小于
.
（I）求ω的取值范围；
（II）在△ABC中，a，b，c分别是内角A，B，C的对边，且a＝1，b＋c＝2，
当ω取最大值时，f(A)＝1，求△ABC的面积.
查看习题详情和答案>>
（本小题满分12分）
已知m＝(cosωx＋sinωx，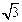
cosωx)，n＝(cosωx－sinωx，2sinωx)，其中ω＞0，若函数f(x)＝m·n，且f(x)的对称中心到f(x)的对称轴的最近距离不小于
.
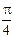（I）求ω的取值范围；
（II）在△ABC中，a，b，c分别是内角A，B，C的对边，且a＝1，b＋c＝2，
当ω取最大值时，f(A)＝1，求△ABC的面积.
已知m＝(cosωx＋sinωx，
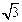cosωx)，n＝(cosωx－sinωx，2sinωx)，其中ω＞0，若函数f(x)＝m·n，且f(x)的对称中心到f(x)的对称轴的最近距离不小于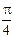.（I）求ω的取值范围；
（II）在△ABC中，a，b，c分别是内角A，B，C的对边，且a＝1，b＋c＝2，
当ω取最大值时，f(A)＝1，求△ABC的面积.
已知函数f(x)＝Asin(ωx＋φ)，(A＞0，ω＞0，∣φ∣＜
，x∈R)的图象的一部分如下图
上的最大值与最小值..