摘要: 对于函数 .若存在.使 成立. 则称为 的“滞点 .已知函数f ( x ) = . (I)试问有无“滞点 ?若有.求之.否则说明理由, (II)已知数列的各项均为负数.且满足,求数列的通项公式, (III)已知,求的前项和. 范水高级中学2005~2006年度第一学期高三数测试题 总分
网址:http://m.1010jiajiao.com/timu3_id_505780[举报]
(本题满分14分)
已知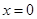 是函数
是函数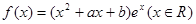 的一个极值点,且函数
的一个极值点,且函数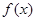 的图象在
的图象在 处的切线的斜率为2
处的切线的斜率为2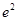 .
.
(Ⅰ)求函数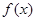 的解析式并求单调区间.(5分)
的解析式并求单调区间.(5分)
(Ⅱ)设 ,其中
,其中 ,问:对于任意的
,问:对于任意的 ,方程
,方程
 在区间
在区间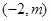 上是否存在实数根?若存在,请确定实数根的个数.若不存在,请说明理由.(9分)
上是否存在实数根?若存在,请确定实数根的个数.若不存在,请说明理由.(9分)
查看习题详情和答案>>
(本题满分14分)已知函数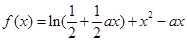 (
(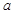 为常数,
为常数,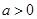 ).
).
(Ⅰ)当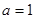 时,求函数
时,求函数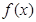 在
在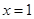 处的切线方程;
处的切线方程;
(Ⅱ)当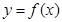 在
在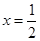 处取得极值时,若关于
处取得极值时,若关于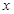 的方程
的方程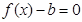 在[0,2]上恰有两个不相等的实数根,求实数
在[0,2]上恰有两个不相等的实数根,求实数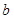 的取值范围;
的取值范围;
(Ⅲ)若对任意的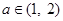 ,总存在
,总存在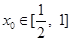 ,使不等式
,使不等式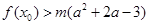 成立,求实数
成立,求实数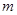 的取值范围.
的取值范围.
查看习题详情和答案>>
(本题满分14分)已知以函数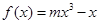 的图象上的点
的图象上的点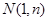 为切点的切线的倾斜角为
为切点的切线的倾斜角为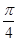 .
.
(1)求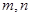 的值;
的值;
(2)是否存在正整数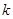 ,使不等式
,使不等式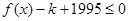 对于
对于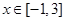 恒成立?若存在,求出最小的正整数
恒成立?若存在,求出最小的正整数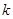 ,若不存在,说明理由;
,若不存在,说明理由;
(3)对于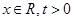 ,比较
,比较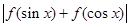 与
与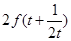 的大小.
的大小.
查看习题详情和答案>>
 是函数
是函数 的一个极值点,且函数
的一个极值点,且函数 的图象在
的图象在 处的切线的斜率为2
处的切线的斜率为2 .
. ,其中
,其中 ,问:对于任意的
,问:对于任意的 ,方程
,方程
 在区间
在区间 上是否存在实数根?若存在,请确定实数根的个数.若不存在,请说明理由.(9分)
上是否存在实数根?若存在,请确定实数根的个数.若不存在,请说明理由.(9分)