摘要：20．集合A是由适合以下性质的函数f (x) 组成的,对于任意的. 上是增函数. (1)试判断?若不在集合A中. 试说明理由, 中你认为是集合A中的函数.不等式是否对于任意的总成立?证明你的结论.

网址：http://m.1010jiajiao.com/timu3_id_505309[举报]

集合A是由适合以下性质的函数f（x）构成的，对于任意的x＞0　y＞0且x≠y都有f（x）+2f（y）＞3f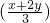 $数学公式$
（1）试判断f₁（x）=log₂x及f₂（x）=（x+1）²是否在集合A中？并说明理由
（2）设f（x）∈A，且定义域是（0，+∞），值域是（1，2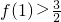）， $数学公式$ ，写出一个满足上述条件的解析式；并证明此函数f（x）∈A．

查看习题详情和答案>>

集合A是由适合以下性质的函数组成：对于任意x≥0，f（x）∈[-2，4]，且f（x）在（0，+∞）上是增函数．
（1）试判断f1(x)=

-2及f2(x)=4-6•(

)x是否在集合A中，并说明理由；
（2）若定义：对定义域中的任意一个x都有不等式f（x）+f（x+2）＜2f（x+1）恒成立，则称这个函数为凸函数．对于（1）中你认为在集合A中的函数f（x）是凸函数吗？试证明你的结论．

查看习题详情和答案>>

集合A是由适合以下性质的函数f（x）组成的，对于任意的x≥0，f（x）∈[-2，4）且f（x）在（0，+∞）上是增函数．
（1）试判断f₁（x）=

-2及f₂（x）=4-6?（

）^x（x≥0）是否在集合A中，若不在集合A中，试说明理由；
（2）对于（1）中你认为是集合A中的函数f（x），不等式f（x）+f（x+2）＜2f（x+1）是否对于任意x≥0总成立？试证明你的结论．查看习题详情和答案>>

集合A是由适合以下性质的函数f（x）构成的：对于定义域内任意两个不相等的实数x₁，x₂，都有

[f(x1)+f(x2)]＞f(

)．
（1）试判断f（x）=x²及g（x）=log₂x是否在集合A中，并说明理由；
（2）设f（x）∈A且定义域为（0，+∞），值域为（0，1），f(1)＞

，试求出一个满足以上条件的函数f （x）的解析式．查看习题详情和答案>>

集合A是由适合以下性质的函数f（x）构成的：对于任意的，且u、υ∈（-1，1），都有|f（u）-f（υ）|≤3|u-υ|．
（1）判断函数f1(x)=

是否在集合A中？并说明理由；
（2）设函数f（x）=ax²+bx，且f（x）∈A，试求2a+b的取值范围；
（3）在（2）的条件下，若f（2）=6，且对于满足（2）的每个实数a，存在最小的实数m，使得当x∈[m，2]时，|f（x）|≤6恒成立，试求用a表示m的表达式．

查看习题详情和答案>>