摘要：(2003年北京朝阳区模拟题)已知椭圆C:+=1(a＞b＞0). (1)若点P(x0.y0)是椭圆C内部的一点.求证:+＜1, (2)若椭圆C:+=1(a＞b＞0)上存在不同的两点关于直线l:y=x+1对称.试求a.b满足的关系式. (1)证明:设F1.F2为椭圆C的左.右两个焦点.∵P是椭圆C内部的一点. ∴|F1P|+|F2P|＜2a. ∴+＜2a. ∴(a2-c2)x02+a2y02＜a2(a2-c2). ∴+＜1(b2=a2-c2). (2)解:设椭圆C上关于直线l对称的点A.B的坐标为A(x1.y1).B(x2.y2).线段AB的中点坐标为M(xM.yM).则有 b2x12+a2y12=a2b2. ① b2x22+a2y22=a2b2. ② =-1. ③ yM=xM+1. ④ ②-①得b2(x22-x12)+a2(y22-y12)=0. b2(x2-x1)(x2+x1)+a2(y2-y1)(y2+y1)=0. b2xM+a2yM=0. 把③代入上式得b2xM-a2yM=0. ⑤ 由④和⑤得xM=.yM=. 即M(.). ∵点M在椭圆C的内部. ∴+＜1. ∴a2+b2＜(b2-a2)2=(a+b)2(a-b)2. a.b应满足的不等式为a2+b2＜(a+b)2(a-b)2.
网址：http://m.1010jiajiao.com/timu3_id_504876[举报]
已知椭圆C：
+
=1(a＞b＞0)，直线y=x+
与以原点为圆心，以椭圆C的短半轴长为半径的圆相切，F1，F2为其左、右焦点，P为椭圆C上任一点，△F1PF2的重心为G，内心为I，且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L：y=kx+m(k≠0)与椭圆C交于不同两点A，B且线段AB的垂直平分线过定点C(
，0)求实数k的取值范围。
查看习题详情和答案>>
已知椭圆C：
+
=1（a＞b＞0）的左右焦点为F1，F2，过F2线与圆x2+y2=b2相切于点A，并与椭圆C交与不同的两点P，Q，如图，PF1⊥PQ，若A为线段PQ的靠近P的三等分点，则椭圆的离心率为（ ）A．
B．
C．
D．
查看习题详情和答案>>
（本题满分14分）已知椭圆C：
=1(a＞b＞0)的离心率为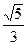
，短轴一
个端点到右焦点的距离为3.
（1）求椭圆C的方程；
（2）过椭圆C上的动点P引圆O：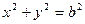
的两条切线PA、PB，A、B分别为切点，试探究椭圆C上是否存在点P，由点P向圆O所引的两条切线互相垂直？若存在，请求出点P的坐标；若不存在，请说明理由.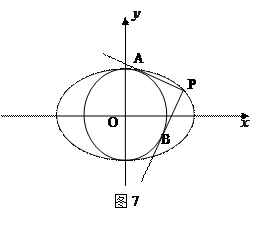
+y2=1(a>1)的上顶点为A,离心率为
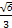,若不过点A的动直线l与椭圆C相交于P,Q两点,且
·
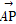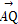=0.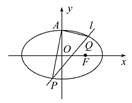
+
=1（a＞b＞0），直线l为圆O：x2+y2=b2的一条切线，记椭圆C的离心率为e．
，且恰好经过椭圆的右顶点，求e的大小；
y+3=0相切，求椭圆方程．