摘要:设点P(x.y)(x≥0)为平面直角坐标系xOy中的一个动点(其中O为坐标原点).点P到定点M(.0)的距离比点P到y轴的距离大. (1)求点P的轨迹方程.并说明它表示什么曲线, (2)若直线l与点P的轨迹相交于A.B两点.且OA⊥OB.点O到直线l的距离为.求直线l的方程. 解:(1)∵x≥0.∴=x+. 整理得y2=2x. 这就是动点P的轨迹方程.它表示顶点在原点.对称轴为x轴.开口向右的一条抛物线. (2)①当直线l的斜率不存在时.由题设可知.直线l的方程是x=. 联立x=与y2=2x.可求得点A.B的坐标分别为(.)与(.-).此时不满足OA⊥OB.故不合题意. ②当直线l的斜率存在时.可设直线l的方程为y=kx+b(其中k≠0.b≠0). 将x=代入y2=2x中. 并整理得ky2-2y+2b=0. ① 设直线l与抛物线的交点坐标为A(x1.y1).B(x2.y2).则y1.y2为方程①的两个根.于是y1y2=. 又由OA⊥OB可得x1x2+y1y2=0. ② 将x1=.x2=代入②并整理得y1y2+4=0.∴b+2k=0. ③ 又由点O到直线l的距离为.得=. ④ 联立③④得k=1.b=-2或k=-1.b=2. 故直线l的方程为y=x-2或y=-x+2.
网址:http://m.1010jiajiao.com/timu3_id_504875[举报]
设点P(x,y)(y≥0)为平面直角坐标系xOy中的一个动点(其中O为坐标原点),点P到定点M(0,
)的距离比点P到x轴的距离大
.
(1)求点P的轨迹方程;
(2)若直线l:y=x+1与点P的轨迹相交于A、B两点,求线段AB的长;
(3)设点P的轨迹是曲线C,点Q(1,y0)是曲线C上一点,求过点Q的曲线C的切线方程. 查看习题详情和答案>>
| 1 |
| 2 |
| 1 |
| 2 |
(1)求点P的轨迹方程;
(2)若直线l:y=x+1与点P的轨迹相交于A、B两点,求线段AB的长;
(3)设点P的轨迹是曲线C,点Q(1,y0)是曲线C上一点,求过点Q的曲线C的切线方程. 查看习题详情和答案>>
设点P(x,y)(x≥0)为平面直角坐标系xOy中的一个动点(其中O为坐标原点),点P到定点M(1,0)的距离比点P到直线x=-2的距离小1,过点M的直线l与点P的轨迹方程交于A、B两点.
(Ⅰ)求点P的轨迹方程;
(Ⅱ)是否存在直线l,使得以线段AB为直径的圆恰好经过坐标原点?若存在,请求出直线l的方程,若不存在,请说明理由.
(III)求证:S△OAB=S△OAM•|BM|.
查看习题详情和答案>>
(Ⅰ)求点P的轨迹方程;
(Ⅱ)是否存在直线l,使得以线段AB为直径的圆恰好经过坐标原点?若存在,请求出直线l的方程,若不存在,请说明理由.
(III)求证:S△OAB=S△OAM•|BM|.
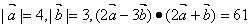 ,求
,求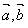 的夹角θ;
的夹角θ;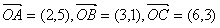 ,若在
,若在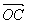 上存在点M,使得
上存在点M,使得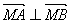 ,求点M的坐标。
,求点M的坐标。