题目内容
设点P(x,y)(x≥0)为平面直角坐标系xOy中的一个动点(其中O为坐标原点),点P到定点M(1,0)的距离比点P到直线x=-2的距离小1,过点M的直线l与点P的轨迹方程交于A、B两点.
(Ⅰ)求点P的轨迹方程;
(Ⅱ)是否存在直线l,使得以线段AB为直径的圆恰好经过坐标原点?若存在,请求出直线l的方程,若不存在,请说明理由.
(III)求证:S△OAB=S△OAM•|BM|.
(Ⅰ)求点P的轨迹方程;
(Ⅱ)是否存在直线l,使得以线段AB为直径的圆恰好经过坐标原点?若存在,请求出直线l的方程,若不存在,请说明理由.
(III)求证:S△OAB=S△OAM•|BM|.
分析:(I)利用抛物线的定义,即可得到点P的轨迹方程;
(Ⅱ)分类讨论,设出直线方程,代入抛物线方程,验证
•
=0是否成立即可;
(III)S△OAB=
•|OM|•|y1-y2|,S△OAM•|BM|=
•|OM|•|y1|•(x2+1),化简可结论.
(Ⅱ)分类讨论,设出直线方程,代入抛物线方程,验证
| OA |
| OB |
(III)S△OAB=
| 1 |
| 2 |
| 1 |
| 2 |
解答:(Ⅰ)解:∵点P到定点M(1,0)的距离比点P(x,y)(x≥0)到直线x=-2的距离小1,
∴由抛物线的定义,可得点P的轨迹方程为y2=4x;
(Ⅱ)解:当直线l的斜率不存在时,由题设可知直线l的方程是x=1,与抛物线方程联立,可得A(1,2),B(1,-2),不满足
•
=0;
当直线l的斜率存在时,设直线l的方程为y=k(x-1),代入抛物线方程,可得k2x2-(2k2+4)x+k2=0
设A(x1,y1),B(x2,y2),
∴x1+x2=
,x1x2=1
∴y1y2=-4,∴x1x2+y1y2=-3≠0,不满足
•
=0
∴不存在直线l,使得以线段AB为直径的圆恰好经过坐标原点;
(III)证明:∵S△OAB=
•|OM|•|y1-y2|=
|y1-y2|=
S△OAM•|BM|=
•|OM|•|y1|•(x2+1)=
•|k(x1-1)|•(x2+1)=
∴S△OAB=S△OAM•|BM|.
∴由抛物线的定义,可得点P的轨迹方程为y2=4x;
(Ⅱ)解:当直线l的斜率不存在时,由题设可知直线l的方程是x=1,与抛物线方程联立,可得A(1,2),B(1,-2),不满足
| OA |
| OB |
当直线l的斜率存在时,设直线l的方程为y=k(x-1),代入抛物线方程,可得k2x2-(2k2+4)x+k2=0
设A(x1,y1),B(x2,y2),
∴x1+x2=
| 2k2+4 |
| k2 |
∴y1y2=-4,∴x1x2+y1y2=-3≠0,不满足
| OA |
| OB |
∴不存在直线l,使得以线段AB为直径的圆恰好经过坐标原点;
(III)证明:∵S△OAB=
| 1 |
| 2 |
| 1 |
| 2 |
| |k(x1-x2)| |
| 2 |
S△OAM•|BM|=
| 1 |
| 2 |
| 1 |
| 2 |
| |k(x1x2+x1-x2-1)| |
| 2 |
| |k(x1-x2)| |
| 2 |
∴S△OAB=S△OAM•|BM|.
点评:本题考查抛物线的定义,考查直线与抛物线的位置关系,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 ,0)的距离比点P到x轴的距离大
,0)的距离比点P到x轴的距离大 .
. =0,点O到直线l的距离为
=0,点O到直线l的距离为 ,求直线l的方程.
,求直线l的方程. ,0)的距离比点P到x轴的距离大
,0)的距离比点P到x轴的距离大 .
.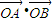 =0,点O到直线l的距离为
=0,点O到直线l的距离为 ,求直线l的方程.
,求直线l的方程.