摘要：设二次函数f(x)=ax2+bx+c(a.b.c∈R且a≠0).若函数y=f(x)的图象与直线y=x和y=-x均无公共点. (1)求证:4ac-b2＞1, (2)求证:对一切实数x.恒有|ax2+bx+c|＞. 证明:(1)方程ax2+bx+c=x和ax2+bx+c=-x均无实根. 即 ①+②得4ac-b2＞1. (2)由4ac-b2＞1.知a(x+)2与同号. 所以|ax2+bx+c|=|a(x+)2+| =|a(x+)2|+||≥||＞.
网址：http://m.1010jiajiao.com/timu3_id_504285[举报]
设二次函数f(x)=ax2+bx+c(a、b、c∈R),且f(1) =-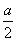
,a＞2c＞b.
,a＞2c＞b.(1)判断a、b的符号;
(2)证明f(x)=0至少有一实根在区间(0,2)内;
(3)求函数y=f(x)图象被x轴所截弦长的范围.
查看习题详情和答案>>设二次函数f(x)=ax2+bx+c(a、b、cÎR)，满足条件：（1）对于任意实数xÎR，f(x-4)=f(2-x)，且f(x)³x；（2）xÎ(0，2)时，有f(x)£
；（3）f(x)在R上的最小值为0．求最大的m(m>1)，使得存在tÎR，只要kÎ[1，m]就有f(x+t)£x．
查看习题详情和答案>>
设二次函数f(x)=ax2+bx+c(a、b、cÎR)，满足条件：（1）对于任意实数xÎR，f(x-4)=f(2-x)，且f(x)³x；（2）xÎ(0，2)时，有f(x)£
；（3）f(x)在R上的最小值为0．求最大的m(m>1)，使得存在tÎR，只要kÎ[1，m]就有f(x+t)£x．
；（3）f(x)在R上的最小值为0．求最大的m(m>1)，使得存在tÎR，只要kÎ[1，m]就有f(x+t)£x．
查看习题详情和答案>>