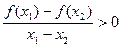摘要： 若函数y=f(x) (xR)满足f.且x=|x|.则函数y=f(x)的图象与函数y=|x|的图象的交点个数为 A．2 B.3 C.4 D.无数个 [解析]∵f是周期为2的函数.在同一坐标系中作出f(x)和y=|x|的图象,即可知选C. [评析]本题考查了数形结合的数学思想.能根据周期性和对称性分别作出两个函数的图象是解答本题的关键.解答本题的难点在于确定y=|x|的图象与f(x)的图象何时起不再会有公共点.显然在y轴右侧,当时.两个图象不再有交点.在高考试题中.往往出现一些判断方程根的个数问题.一般也可将方程恰当变形(变形的依据是.变形后易于作出等号两边的函数图象)后.将等式两边分别看作两个函数.把方程的根的个数问题转化为图象的交点个数问题.如的实根个数有多少个?变形为.令.在x>10时.两个图象不再有公共点.作出图象后可知交点只有三个.故原方程的实数解有且仅有3个.
网址：http://m.1010jiajiao.com/timu3_id_504209[举报]
(2007
辽宁，21)已知数列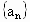
、
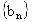与函数f(x)、g(x)，x
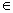R满足条件：
，
．
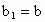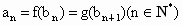(1)
若f(x)=tx＋1(t≠0，t≠2)，g(x)=2x，f(b)≠g(b)，且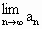
存在，求t的取值范围，并求
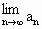(用t表示)；
(2)
若函数y=f(x)为R上的增函数，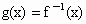
，b=1，f(1)＜1，证明对任意的
，
．
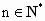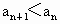查看习题详情和答案>>
定义在R上的偶函数y=f(x)满足：
①对x
R都有f(x+6)=f(x)+f(3)
②f(－5)=－1;
③当x1,x2[0,3]且x1≠x2时，都有
则（1）f(2009)=_______________；
（2）若方程f(x)=0在区间[a,6－a]上恰有3个不同实根，实数a的取值范围是____________。
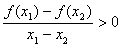
R都有f(x+6)=f(x)+f(3)
R都有f(x+6)=f(x)+f(3)