摘要: (2005山东卷理第22题.文第22题) 已知动圆过定点.且与直线相切.其中. (I)求动圆圆心的轨迹的方程, 设A.B是轨迹上异于原点的两个不同点.直线和的倾斜角分别为和.当变化且为定值时.证明直线恒过定点.并求出该定点的坐标. 设A.B是轨迹上异于原点的两个不同点.直线和的倾斜角分别为和.当变化且时.证明直线恒过定点.并求出该定点的坐标
网址:http://m.1010jiajiao.com/timu3_id_503552[举报]
已知动圆过定点(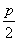 ,0),且与直线x=
,0),且与直线x=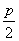 相切,其中p>0.
相切,其中p>0.
(1)求动圆圆心C的轨迹方程;
(2)设A、B是轨迹C上异于原点O的两个不同点,直线OA和OB的倾斜角分别为α和β,当α、β变化且α+β为定值θ(0<θ<π)时,证明直线AB恒过定点,并求出该定点的坐标.
查看习题详情和答案>> ,且与定直线
,且与定直线 相切.
相切. 的方程;
的方程; 是轨迹
是轨迹 、
、 为切点作轨迹
为切点作轨迹 ,证明:
,证明: .
. ,且与直线
,且与直线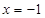 相切.
相切. 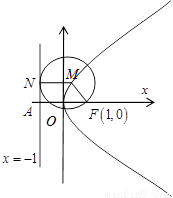
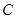 的方程;
的方程;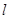 :
: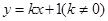 ,并与轨迹
,并与轨迹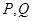 两点,且满足
两点,且满足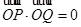 ?若存在,求出直线
?若存在,求出直线