摘要:16.对任意.函数的值总大于0.则的取值范围是( ) (A) {│} (B) {│} (C) {│} (D) {│}
网址:http://m.1010jiajiao.com/timu3_id_503456[举报]
设函数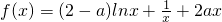 ;(a∈R).
;(a∈R).
(1)当a=0时,求f(x)的极值.(2)当a≠0时,求f(x)的单调区间.(3)当a=2时,对于任意正整数n,在区间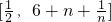 上总存在m+4个数a1,a2,a3,…,am,am+1,am+2,am+3,am+4,使得f(a1)+f(a2)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立,试问:正整数m是否有最大值?若有求其最大值;否则,说明理由.
上总存在m+4个数a1,a2,a3,…,am,am+1,am+2,am+3,am+4,使得f(a1)+f(a2)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立,试问:正整数m是否有最大值?若有求其最大值;否则,说明理由.
查看习题详情和答案>>
设函数 ;(a∈R).
;(a∈R).
(1)当a=0时,求f(x)的极值.(2)当a≠0时,求f(x)的单调区间.(3)当a=2时,对于任意正整数n,在区间 上总存在m+4个数a1,a2,a3,…,am,am+1,am+2,am+3,am+4,使得f(a1)+f(a2)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立,试问:正整数m是否有最大值?若有求其最大值;否则,说明理由.
上总存在m+4个数a1,a2,a3,…,am,am+1,am+2,am+3,am+4,使得f(a1)+f(a2)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立,试问:正整数m是否有最大值?若有求其最大值;否则,说明理由.
查看习题详情和答案>>
 ;(a∈R).
;(a∈R).(1)当a=0时,求f(x)的极值.(2)当a≠0时,求f(x)的单调区间.(3)当a=2时,对于任意正整数n,在区间
 上总存在m+4个数a1,a2,a3,…,am,am+1,am+2,am+3,am+4,使得f(a1)+f(a2)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立,试问:正整数m是否有最大值?若有求其最大值;否则,说明理由.
上总存在m+4个数a1,a2,a3,…,am,am+1,am+2,am+3,am+4,使得f(a1)+f(a2)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立,试问:正整数m是否有最大值?若有求其最大值;否则,说明理由.查看习题详情和答案>>
设函数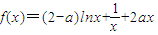 ;(a∈R).
;(a∈R).
(1)当a=0时,求f(x)的极值.(2)当a≠0时,求f(x)的单调区间.(3)当a=2时,对于任意正整数n,在区间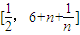 上总存在m+4个数a1,a2,a3,…,am,am+1,am+2,am+3,am+4,使得f(a1)+f(a2)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立,试问:正整数m是否有最大值?若有求其最大值;否则,说明理由.
上总存在m+4个数a1,a2,a3,…,am,am+1,am+2,am+3,am+4,使得f(a1)+f(a2)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立,试问:正整数m是否有最大值?若有求其最大值;否则,说明理由.
查看习题详情和答案>>
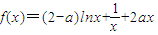 ;(a∈R).
;(a∈R).(1)当a=0时,求f(x)的极值.(2)当a≠0时,求f(x)的单调区间.(3)当a=2时,对于任意正整数n,在区间
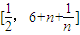 上总存在m+4个数a1,a2,a3,…,am,am+1,am+2,am+3,am+4,使得f(a1)+f(a2)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立,试问:正整数m是否有最大值?若有求其最大值;否则,说明理由.
上总存在m+4个数a1,a2,a3,…,am,am+1,am+2,am+3,am+4,使得f(a1)+f(a2)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立,试问:正整数m是否有最大值?若有求其最大值;否则,说明理由.查看习题详情和答案>>
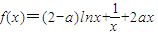 ;(a∈R).
;(a∈R).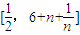 上总存在m+4个数a1,a2,a3,…,am,am+1,am+2,am+3,am+4,使得f(a1)+f(a2)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立,试问:正整数m是否有最大值?若有求其最大值;否则,说明理由.
上总存在m+4个数a1,a2,a3,…,am,am+1,am+2,am+3,am+4,使得f(a1)+f(a2)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立,试问:正整数m是否有最大值?若有求其最大值;否则,说明理由.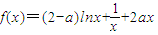 ;(a∈R).
;(a∈R).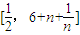 上总存在m+4个数a1,a2,a3,…,am,am+1,am+2,am+3,am+4,使得f(a1)+f(a2)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立,试问:正整数m是否有最大值?若有求其最大值;否则,说明理由.
上总存在m+4个数a1,a2,a3,…,am,am+1,am+2,am+3,am+4,使得f(a1)+f(a2)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立,试问:正整数m是否有最大值?若有求其最大值;否则,说明理由.