摘要:44..在已知向量长度求两向量夹角时注意用此关系整体求得数量积.
网址:http://m.1010jiajiao.com/timu3_id_503169[举报]
本题包括高考A,B,C,D四个选题中的B,C两个小题,每小题10分,共20分.把答案写在答题卡相应的位置上.解答时应写出文字说明、证明过程或演算步骤.
B.选修4-2:矩阵与变换
已知矩阵A=
,向量
=
.求向量
,使得A2
=
.
C.选修4-4:极坐标与参数方程
在直角坐标系x0y中,直线l的参数方程为
(t为参数),若以直角坐标系xOy的O点为极点,Ox为极轴,且长度单位相同,建立极坐标系,得曲线C的极坐标方程为ρ=2cos(θ-
).
(1)求直线l的倾斜角;
(2)若直线l与曲线l交于A、B两点,求AB.
查看习题详情和答案>>
B.选修4-2:矩阵与变换
已知矩阵A=
|
| β |
|
| α |
| α |
| β |
C.选修4-4:极坐标与参数方程
在直角坐标系x0y中,直线l的参数方程为
|
| π |
| 4 |
(1)求直线l的倾斜角;
(2)若直线l与曲线l交于A、B两点,求AB.
已知椭圆C的两个焦点分别为F1(-1,0),F2(1,0),点M(1,
)在椭圆C上,抛物线E以椭圆C的中心为顶点,F2为焦点.
(1)求椭圆C的方程;
(2)直线l过点F2,且交y轴于D点,交抛物线E于A,B两点.
①若F1B⊥F2B,求|AF2|-|BF2|的值;
②试探究:线段AB与F2D的长度能否相等?如果|AB|=|F2D|,求直线l的方程.
查看习题详情和答案>>
| 3 | 2 |
(1)求椭圆C的方程;
(2)直线l过点F2,且交y轴于D点,交抛物线E于A,B两点.
①若F1B⊥F2B,求|AF2|-|BF2|的值;
②试探究:线段AB与F2D的长度能否相等?如果|AB|=|F2D|,求直线l的方程.
 给定椭圆C:
给定椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| a2+b2 |
(1)若椭圆C过点(
| 5 |
(2)如果直线x+y=3
| 2 |
(3)已知椭圆C的两个焦点分别是F1(-
| 2 |
| 2 |
| M1F1 |
| M1F |
| 3 |
| MN |
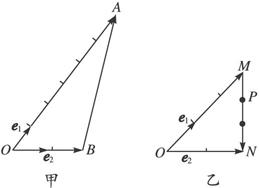
 中,
中,  分别是
分别是 的对边,
的对边, 是方程
是方程 的两个根,且
的两个根,且 .
.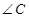 的度数和
的度数和 的长度.
的长度.