摘要:24.用求数列的通项公式时.an一般是分段形式对吗?你注意到了吗?
网址:http://m.1010jiajiao.com/timu3_id_503149[举报]
在等差数列![]() 中,
中,![]() ,
,![]() ,其中
,其中![]() 是数列
是数列![]() 的前
的前![]() 项之和,曲线
项之和,曲线![]() 的方程是
的方程是![]() ,直线
,直线![]() 的方程是
的方程是![]() .
.
求数列![]() 的通项公式;
的通项公式;
当直线![]() 与曲线
与曲线![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() 时,令
时,令![]() ,
,
求![]() 的最小值;
的最小值;
对于直线![]() 和直线外的一点P,用“
和直线外的一点P,用“![]() 上的点与点P距离的最小值”定义点P到直线
上的点与点P距离的最小值”定义点P到直线![]() 的距离与原有的点到直线距离的概念是等价的,若曲线
的距离与原有的点到直线距离的概念是等价的,若曲线![]() 与直线
与直线![]() 不相交,试以类似的方式给出一条曲线
不相交,试以类似的方式给出一条曲线![]() 与直线
与直线![]() 间“距离”的定义,并依照给出的定义,在
间“距离”的定义,并依照给出的定义,在![]() 中自行选定一个椭圆,求出该椭圆与直线
中自行选定一个椭圆,求出该椭圆与直线![]() 的“距离”.
的“距离”.
(09年东城区二模理)(14分)
已知函数![]() =
=![]() (其中
(其中![]() 为常数,
为常数,![]() ).利用函数
).利用函数![]() 构造一个数列
构造一个数列![]() ,方法如下:
,方法如下:
对于给定的定义域中的![]() ,令
,令![]() ,
,![]() ,…,
,…,![]() ,…
,…
在上述构造过程中,如果![]() (
(![]() =1,2,3,…)在定义域中,那么构造数列的过程继续下去;如果
=1,2,3,…)在定义域中,那么构造数列的过程继续下去;如果![]() 不在定义域中,那么构造数列的过程就停止.
不在定义域中,那么构造数列的过程就停止.
(Ⅰ)当![]() 且
且![]() 时,求数列
时,求数列![]() 的通项公式;
的通项公式;
(Ⅱ)如果可以用上述方法构造出一个常数列,求![]() 的取值范围;
的取值范围;
在等差数列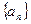 中,
中,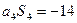 ,
,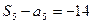 ,其中
,其中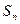 是数列
是数列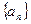 的前
的前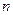 项之和,曲线
项之和,曲线 的方程是
的方程是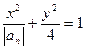 ,直线
,直线 的方程是
的方程是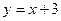 .
.
(1) 求数列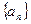 的通项公式;
的通项公式;
(2) 当直线 与曲线
与曲线 相交于不同的两点
相交于不同的两点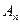 ,
,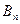 时,令
时,令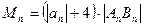 ,
,
求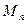 的最小值;
的最小值;
(3) 对于直线 和直线外的一点P,用“
和直线外的一点P,用“ 上的点与点P距离的最小值”定义点P到直线
上的点与点P距离的最小值”定义点P到直线 的距离与原有的点到直线距离的概念是等价的,若曲线
的距离与原有的点到直线距离的概念是等价的,若曲线 与直线
与直线 不相交,试以类似的方式给出一条曲线
不相交,试以类似的方式给出一条曲线 与直线
与直线 间“距离”的定义,并依照给出的定义,在
间“距离”的定义,并依照给出的定义,在 中自行选定一个椭圆,求出该椭圆与直线
中自行选定一个椭圆,求出该椭圆与直线 的“距离”.
的“距离”.
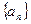 中,
中,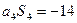 ,
,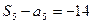 ,其中
,其中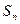 是数列
是数列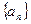 的前
的前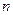 项之和,曲线
项之和,曲线 的方程是
的方程是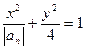 ,直线
,直线 的方程是
的方程是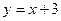 .
.(1) 求数列
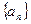 的通项公式;
的通项公式;(2) 当直线
 与曲线
与曲线 相交于不同的两点
相交于不同的两点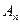 ,
,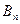 时,令
时,令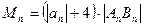 ,
,求
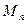 的最小值;
的最小值;(3) 对于直线
 和直线外的一点P,用“
和直线外的一点P,用“ 上的点与点P距离的最小值”定义点P到直线
上的点与点P距离的最小值”定义点P到直线 的距离与原有的点到直线距离的概念是等价的,若曲线
的距离与原有的点到直线距离的概念是等价的,若曲线 与直线
与直线 不相交,试以类似的方式给出一条曲线
不相交,试以类似的方式给出一条曲线 与直线
与直线 间“距离”的定义,并依照给出的定义,在
间“距离”的定义,并依照给出的定义,在 中自行选定一个椭圆,求出该椭圆与直线
中自行选定一个椭圆,求出该椭圆与直线 的“距离”.
的“距离”.