摘要:21.等比数列的一个求和公式:设等比数列的前n项和为.公比为, 则 .
网址:http://m.1010jiajiao.com/timu3_id_503146[举报]
设等比数列{an}的前n项和为Sn,已知an+1=2Sn+2(n∈N+).
(1)求数列{an}通项公式;
(2)在an与an+1之间插入n个数,使这n+2个数组成一个公差为dn的等差数列.
(ⅰ)求证:
+
+
+…+
<
(n∈N+)
(ⅱ)在数列{dn}中是否存在三项dm,dk,dp(其中m,k,p成等差数列)成等比数列.
查看习题详情和答案>>
(1)求数列{an}通项公式;
(2)在an与an+1之间插入n个数,使这n+2个数组成一个公差为dn的等差数列.
(ⅰ)求证:
| 1 |
| d1 |
| 1 |
| d2 |
| 1 |
| d3 |
| 1 |
| dn |
| 15 |
| 16 |
(ⅱ)在数列{dn}中是否存在三项dm,dk,dp(其中m,k,p成等差数列)成等比数列.
设等比数列{an}的首项为a,公比q>0且q≠1,前n项和为Sn.
(Ⅰ)当a=1时,S1+1,S2+2,S3+1三数成等差数列,求数列{an}的通项公式;
(Ⅱ)对任意正整数n,命题甲:Sn,(Sn+1+1),Sn+2三数构成等差数列. 命题乙:Sn+1,(Sn+2+1),Sn+3三数构成等差数列.求证:对于同一个正整数n,命题甲与命题乙不能同时为真命题.
查看习题详情和答案>>
(Ⅰ)当a=1时,S1+1,S2+2,S3+1三数成等差数列,求数列{an}的通项公式;
(Ⅱ)对任意正整数n,命题甲:Sn,(Sn+1+1),Sn+2三数构成等差数列. 命题乙:Sn+1,(Sn+2+1),Sn+3三数构成等差数列.求证:对于同一个正整数n,命题甲与命题乙不能同时为真命题.
设等比数列 的前n项和为Sn,已知
的前n项和为Sn,已知
(1)求数列 通项公式;
通项公式;
(2)在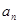 与
与 之间插入n个数,使这n+2个数组成一个公差为
之间插入n个数,使这n+2个数组成一个公差为 的等差数列。
的等差数列。
(Ⅰ)求证:
(Ⅱ)在数列 中是否存在三项
中是否存在三项 (其中m,k,p成等差数列)成等比数列,若存在,求出这样的三项;若不存在,说明理由
(其中m,k,p成等差数列)成等比数列,若存在,求出这样的三项;若不存在,说明理由
查看习题详情和答案>>
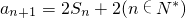 .
.