摘要:22.(本题满分18分.其中第小题6分.第 如图所示.是树形图形.第一层是一条与水平线垂直的线段.长度为1,第二层在第一层线段的前端作两条与该段均成1350的线段.长度为其一半,第三层按第二层的方法在每一线段的前端生成两条线段,重复前面的作法作图至第n层.设树形图的第n层的最高点到水平线的距离为第n层树形图的高度. 1)求第三层及第四层树形图的高度H3.H4, 2)求第n层树形图的高度Hn, 3)若树形图的高度大于2.则称树形图为“高大 .否则称为“矮小 .显然.当时是“矮小 的.是否存在.使得当时.该树形图是“高大 的?
网址:http://m.1010jiajiao.com/timu3_id_502486[举报]
(本题满分18分,其中第1小题6分,第2小题6分,第3小题6分)
已知数列![]() 的首项为1,前
的首项为1,前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,![]() .数列
.数列![]() 满足
满足![]() .
.
(1) 求数列![]() 的通项公式;
的通项公式;
(2) 当![]() 时,试比较
时,试比较![]() 与
与![]() 的大小,并说明理由;
的大小,并说明理由;
(3) 试判断:当![]() 时,向量
时,向量![]()
![]() 是否可能恰为直线
是否可能恰为直线![]()
![]() 的方向向量?请说明你的理由.
的方向向量?请说明你的理由.
(本题满分18分,其中第1小题6分,第2小题4分,第3小题8分)
现有变换公式![]() :
: 可把平面直角坐标系上的一点
可把平面直角坐标系上的一点![]() 变换到这一平面上的一点
变换到这一平面上的一点![]() .
.
(1)若椭圆![]() 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在![]() 轴上,且焦距为
轴上,且焦距为![]() ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆![]() 的标准方程,并求出其两个焦点
的标准方程,并求出其两个焦点![]() 、
、![]() 经变换公式
经变换公式![]() 变换后得到的点
变换后得到的点![]() 和
和![]() 的坐标;
的坐标;
(2) 若曲线![]() 上一点
上一点![]() 经变换公式
经变换公式![]() 变换后得到的点
变换后得到的点![]() 与点
与点![]() 重合,则称点
重合,则称点![]() 是曲线
是曲线![]() 在变换
在变换![]() 下的不动点. 求(1)中的椭圆
下的不动点. 求(1)中的椭圆![]() 在变换
在变换![]() 下的所有不动点的坐标;
下的所有不动点的坐标;
(3) 在(2)的基础上,试探究:中心为坐标原点、对称轴为坐标轴的椭圆和双曲线在变换![]() 下的不动点的存在情况和个数.
下的不动点的存在情况和个数.
(本题满分18分,其中第1小题6分,第2小题4分,第3小题8分)
定义变换![]() :
:![]() 可把平面直角坐标系上的点
可把平面直角坐标系上的点![]() 变换到这一平面上的点
变换到这一平面上的点![]() .特别地,若曲线
.特别地,若曲线![]() 上一点
上一点![]() 经变换公式
经变换公式![]() 变换后得到的点
变换后得到的点![]() 与点
与点![]() 重合,则称点
重合,则称点![]() 是曲线
是曲线![]() 在变换
在变换![]() 下的不动点.
下的不动点.
(1)若椭圆![]() 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在![]() 轴上,且焦距为
轴上,且焦距为![]() ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆![]() 的标准方程. 并求出当
的标准方程. 并求出当![]() 时,其两个焦点
时,其两个焦点![]() 、
、![]() 经变换公式
经变换公式![]() 变换后得到的点
变换后得到的点![]() 和
和![]() 的坐标;
的坐标;
(2)当![]() 时,求(1)中的椭圆
时,求(1)中的椭圆![]() 在变换
在变换![]() 下的所有不动点的坐标;
下的所有不动点的坐标;
(3)试探究:中心为坐标原点、对称轴为坐标轴的双曲线在变换
![]() :
:![]() (
(![]() ,
,![]() )下的不动点的存在情况和个数.
)下的不动点的存在情况和个数.
 的首项为1,前
的首项为1,前 项和为
项和为 ,且满足
,且满足 ,
, .数列
.数列 满足
满足 .
.  时,试比较
时,试比较 与
与 的大小,并说明理由;
的大小,并说明理由;
 是否可能恰为直线
是否可能恰为直线
 的方向向量?请说明你的理由.
的方向向量?请说明你的理由. :
: 可把平面直角坐标系上的点
可把平面直角坐标系上的点 变换到这一平面上的点
变换到这一平面上的点 .特别地,若曲线
.特别地,若曲线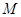 上一点
上一点 经变换公式
经变换公式 与点
与点 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在 轴上,且焦距为
轴上,且焦距为 ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆 时,其两个焦点
时,其两个焦点 、
、 经变换公式
经变换公式 和
和 的坐标;
的坐标; ,
, )下的不动点的存在情况和个数.
)下的不动点的存在情况和个数.