摘要：函数的导函数在区间[0.1]上存在反函数的充要条件是
网址：http://m.1010jiajiao.com/timu3_id_502087[举报]
设函数f（x）定义在（0，+∞）上，f（1）=0，导函数f′（x）=
，g（x）=f（x）+f′（x）．
（Ⅰ）求g（x）的单调区间和最小值；
（Ⅱ）讨论g（x）与g(
)的大小关系；
（Ⅲ）是否存在x0＞0，使得|g（x）-g（x0）|＜
对任意x＞0成立？若存在，求出x0的取值范围；若不存在请说明理由．
查看习题详情和答案>>
| 1 |
| x |
（Ⅰ）求g（x）的单调区间和最小值；
（Ⅱ）讨论g（x）与g(
| 1 |
| x |
（Ⅲ）是否存在x0＞0，使得|g（x）-g（x0）|＜
| 1 |
| x |
设函数设函数f（x）定义在（0，+∞）上，f（1）=0，导函数f′(x)=
，g（x）=f（x）+f'（x）．
（1）求g（x）的单调区间和最小值；
（2）讨论g（x）与g(
)的大小关系；
（3）是否存在x0＞0，使得|g(x)-g(x0)|＜
对任意x＞0成立？若存在，求出x0的取值范围；若不存在，请说明理由．
查看习题详情和答案>>
| 1 |
| x |
（1）求g（x）的单调区间和最小值；
（2）讨论g（x）与g(
| 1 |
| x |
（3）是否存在x0＞0，使得|g(x)-g(x0)|＜
| 1 |
| x |
设函数f(x)定义在(0，＋∞)上，f(1)＝0，导函数
，
．
(1)求g(x)的单调区间和最小值；
(2)讨论g(x)与
的大小关系；
(3)是否存在x0＞0，使得
对任意x＞0成立？若存在，求出x0的取值范围；若不存在，请说明理由．
，
.
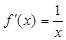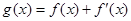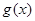的单调区间和最小值；
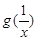的大小关系；
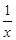对任意x＞0成立？若存在，求出x0的取值范围；若不存在请说明理由．
，
.
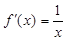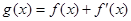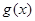的单调区间和最小值；
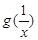的大小关系；
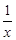对任意x＞0成立？若存在，求出x0的取值范围；若不存在请说明理由．