若对于任意的.函数的值恒为正.则的取值范围是 .——青夏教育精英家教网——

摘要：若对于任意的.函数的值恒为正.则的取值范围是 .

网址：http://m.1010jiajiao.com/timu3_id_501985[举报]

若对于定义在R上的函数f（x），其图象是连续不断的，且存在常数λ（λ∈R），使得f（x+λ）+λf（x）=0对任意的实数x恒成立，则称f（x）是“λ-同伴函数”．下列关于“λ-同伴函数”的命题：
①“

-同伴函数”至少有一个零点；
②f（x）=x²是“λ-同伴函数”；
③f（x）=2^x是“λ-同伴函数”；
④f（x）=0是唯一一个常值“λ-同伴函数”．
其中正确的命题个数为（）
A．1
B．2
C．3
D．4
查看习题详情和答案>>

函数y=f（x）的定义域D={x|x∈R，且x≠0}，对定义域D内任意两个实数x₁，x₂，都有f（x₁）+f（x₂）=f（x₁x₂）成立．
（1）求f（-1）的值并证明y=f（x）为偶函数；
（2）若f（-4）=4，记 an=(-1)n•f(2n)

&(n∈N，n≥1)

，求数列{a_n}的前2009项的和S₂₀₀₉；
（3）（理）若x＞1时，f（x）＜0，且不等式f(

)+f(a)对任意正实数x，y恒成立，求非零实数a的取值范围．
（4）（文）若x＞1时，f（x）＜0，解关于x的不等式 f（x-3）≥0．

查看习题详情和答案>>

函数y=f（x）的定义域D={x|x∈R，且x≠0}，对定义域D内任意两个实数x₁，x₂，都有f（x₁）+f（x₂）=f（x₁x₂）成立．
（1）求f（-1）的值并证明y=f（x）为偶函数；
（2）若f（-4）=4，记 an=(-1)n•f(2n)

&(n∈N，n≥1)

，求数列{a_n}的前2009项的和S₂₀₀₉；
（3）（理）若x＞1时，f（x）＜0，且不等式f(

)+f(a)对任意正实数x，y恒成立，求非零实数a的取值范围．
（4）（文）若x＞1时，f（x）＜0，解关于x的不等式 f（x-3）≥0．

查看习题详情和答案>>

对于定义在区间D上的函数f（X），若存在闭区间[a，b]?D和常数c，使得对任意x₁∈[a，b]，都有f（x₁）=c，且对任意x₂∈D，当x₂∉[a，b]时，f（x₂）＜c恒成立，则称函数f（x）为区间D上的“平顶型”函数．给出下列说法：
①“平顶型”函数在定义域内有最大值；
②函数f（x）=x-|x-2|为R上的“平顶型”函数；
③函数f（x）=sinx-|sinx|为R上的“平顶型”函数；
④当t≤

时，函数，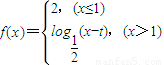

是区间[0，+∞）上的“平顶型”函数．
其中正确的是．（填上你认为正确结论的序号）查看习题详情和答案>>

对于定义在区间D上的函数f（X），若存在闭区间[a，b]?D和常数c，．使得对任意x₁∈[a，b]，都有f（x₁）=c，且对任意x₂∈D，当x₂∉[a，b]时，f（x₂）＜c恒成立，则称函数f（X）为区间D上的“平顶型”函数．给出下列说法：
①“平顶型”函数在定义域内有最大值；
②“平顶型”函数在定义域内一定没有最小值；
③函数f（x）=-|x+2|-|x-1|为R上的“平顶型”函数；
④函数f（x）=sinx-|sinx|为R上的“平顶型”函数．
则以上说法中正确的是．（填上你认为正确结论的序号）查看习题详情和答案>>