题目内容
对于定义在区间D上的函数f(X),若存在闭区间[a,b]?D和常数c,使得对任意x1∈[a,b],都有f(x1)=c,且对任意x2∈D,当x2∉[a,b]时,f(x2)<c恒成立,则称函数f(x)为区间D上的“平顶型”函数.给出下列说法:①“平顶型”函数在定义域内有最大值;
②函数f(x)=x-|x-2|为R上的“平顶型”函数;
③函数f(x)=sinx-|sinx|为R上的“平顶型”函数;
④当t≤
 时,函数,
时,函数,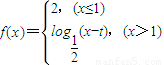 是区间[0,+∞)上的“平顶型”函数.
是区间[0,+∞)上的“平顶型”函数.其中正确的是 .(填上你认为正确结论的序号)
【答案】分析:根据题意,“平顶型”函数在定义域内某个子集区间内函数值为常数c,且这个常数是函数的最大值,但是定义并没有指出函数最小值的情况.由此定义再结合绝对值的性质和正弦函数的图象与性质,对于四个选项逐个加以判断,即得正确答案.
解答:解:对于①,根据题意,“平顶型”函数在定义域内某个子集区间内函数值为常数c,且这个常数是函数的最大值,故①正确.
对于②,函数f(x)=x-|x-2|=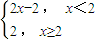 ,当且仅当x∈[2,+∞)时,函数的最大值为2,符合“平顶型”函数的定义,故②正确.
,当且仅当x∈[2,+∞)时,函数的最大值为2,符合“平顶型”函数的定义,故②正确.
对于③,函数f(x)=sinx-|sinx|=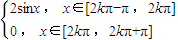 ,但是不存在区间[a,b],对任意x1∈[a,b],都有f(x1)=2,
,但是不存在区间[a,b],对任意x1∈[a,b],都有f(x1)=2,
所以f(x)不是“平顶型”函数,故③不正确.
对于④当t≤ 时,函数,
时,函数,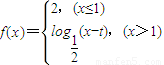 ,当且仅当x∈(-∞,1]时,函数的最大值为2,符合“平顶型”函数的定义,故④正确.
,当且仅当x∈(-∞,1]时,函数的最大值为2,符合“平顶型”函数的定义,故④正确.
故答案为 ①②④.
点评:本题以命题真假的判断为载体,着重考查了函数的最值及其几何意义、带绝对值的函数和正弦函数的定义域值域等知识点,属于中档题.
解答:解:对于①,根据题意,“平顶型”函数在定义域内某个子集区间内函数值为常数c,且这个常数是函数的最大值,故①正确.
对于②,函数f(x)=x-|x-2|=
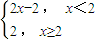 ,当且仅当x∈[2,+∞)时,函数的最大值为2,符合“平顶型”函数的定义,故②正确.
,当且仅当x∈[2,+∞)时,函数的最大值为2,符合“平顶型”函数的定义,故②正确.对于③,函数f(x)=sinx-|sinx|=
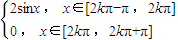 ,但是不存在区间[a,b],对任意x1∈[a,b],都有f(x1)=2,
,但是不存在区间[a,b],对任意x1∈[a,b],都有f(x1)=2,所以f(x)不是“平顶型”函数,故③不正确.
对于④当t≤
 时,函数,
时,函数,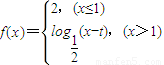 ,当且仅当x∈(-∞,1]时,函数的最大值为2,符合“平顶型”函数的定义,故④正确.
,当且仅当x∈(-∞,1]时,函数的最大值为2,符合“平顶型”函数的定义,故④正确.故答案为 ①②④.
点评:本题以命题真假的判断为载体,着重考查了函数的最值及其几何意义、带绝对值的函数和正弦函数的定义域值域等知识点,属于中档题.

练习册系列答案
相关题目