摘要:(1).由已知在[0.1]上大于等于0.在[1.2]上小于 等于0.∴x=1为极大值点. (2)由.有三个相异实根. 且 (3)在[1.2]上为减函数.∴最大值为.∴只有 上恒成立即可 恒成立.又. 的最大值为-2.
网址:http://m.1010jiajiao.com/timu3_id_501929[举报]
 已知焦点在x轴上的椭圆C过点(0,1),且离心率为
已知焦点在x轴上的椭圆C过点(0,1),且离心率为
| ||
| 2 |
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)已知过点(-
| 6 |
| 5 |
(ⅰ)若直线l垂直于x轴,求∠AQB的大小;
(ⅱ)若直线l与x轴不垂直,是否存在直线l使得△QAB为等腰三角形?如果存在,求出直线l的方程;如果不存在,请说明理由.
已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,离心率为
,离心率为 ,P是椭圆上一点,且
,P是椭圆上一点,且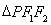 面积的最大值等于2.
面积的最大值等于2.
(1)求椭圆的方程;
(2)过点M(0,2)作直线 与直线
与直线 垂直,试判断直线
垂直,试判断直线 与椭圆的位置关系5
与椭圆的位置关系5
(3)直线y=2上是否存在点Q,使得从该点向椭圆所引的两条切线相互垂直?若存在,求点Q的坐标;若不存在,说明理由。
查看习题详情和答案>>
已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,离心率为
,离心率为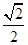 ,P是椭圆上一点,且
,P是椭圆上一点,且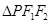 面积的最大值等于2.
面积的最大值等于2.
(1)求椭圆的方程;
(2)过点M(0,2)作直线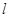 与直线
与直线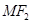 垂直,试判断直线
垂直,试判断直线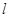 与椭圆的位置关系5
与椭圆的位置关系5
(3)直线y=2上是否存在点Q,使得从该点向椭圆所引的两条切线相互垂直?若存在,求点Q的坐标;若不存在,说明理由。
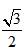 ,Q为椭圆C的左顶点。
,Q为椭圆C的左顶点。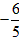 ,0)的直线l与椭圆C交于A,B两点。
,0)的直线l与椭圆C交于A,B两点。