题目内容
已知:双曲线的顶点坐标(0,1),(0,-l),离心率![]() ,又抛物线
,又抛物线![]() 的焦点与双曲线一个焦点重合.
的焦点与双曲线一个焦点重合.
(1)求抛物线![]() 的方程;
的方程;
(2)已知![]() 是
是![]() 轴上的两点,过
轴上的两点,过![]() 做直线与抛物线
做直线与抛物线![]() 交于
交于![]() 两点,试证:直线
两点,试证:直线![]() 与
与![]() 轴所成的锐角相等.
轴所成的锐角相等.
(3)在(2)的前提下,若直线![]() 的斜率为1,问
的斜率为1,问![]() 的面积是否有最大值?若有,求出最大值.若没有,说明理由.
的面积是否有最大值?若有,求出最大值.若没有,说明理由.
(1)![]() (2)略
(2)略
解析:
(1)由题意,设双曲线方程为![]() ,则
,则![]() 解得
解得![]() ------2分
------2分
所以双曲线两焦点为![]() ,即
,即![]() 故
故![]() ,
,
∴抛物线![]() 的方程为
的方程为![]() ;-----------------5分
;-----------------5分
(2)设直线AB方程为![]() ,代入抛物线
,代入抛物线![]() 的方程为
的方程为![]() 得:
得:
![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() -----------------7分
-----------------7分
要证直线![]() 与
与![]() 轴所成的锐角相等,只证明
轴所成的锐角相等,只证明![]() ,
,
∵![]()
![]()
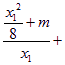
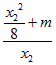 =
=![]() ,
,
所以原命题成立.-------------------9分
(3)由(2)知,k=1时,![]() 化为
化为![]() ,由
,由![]() 得
得![]() ,
,
![]() 点Q到AB的距离为
点Q到AB的距离为![]() ,---------10分
,---------10分
![]() -----------11分
-----------11分
令![]() ,则
,则![]() ,令
,令![]() 得:
得:
![]() ,
,
∴![]() 在
在![]() 和(0,
和(0,![]() 上都是增函数,
上都是增函数,
在![]() 是减函数,------------13分
是减函数,------------13分
所以![]() 无最大值.----------------14分
无最大值.----------------14分

练习册系列答案
相关题目
 ,它们在
,它们在 轴上有共同焦点,抛物线的顶点为坐
轴上有共同焦点,抛物线的顶点为坐