摘要： 如图所示. VAD是边长为2的等边三角形,ABCD是正方形, 平面VAD平面ABCD,E为VC中点． (Ⅰ)求VC与平面ABCD所成角的余弦值, (Ⅱ)求D到平面VBC的距离, (Ⅲ)在边AB上是否存在一点F.使DE面VCF.若存在.求出点F的位置,若不存在.说明理由．
网址：http://m.1010jiajiao.com/timu3_id_501867[举报]
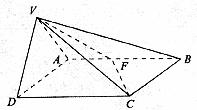
如图所示，△VAD是等边三角形，ABCD是矩形，
，平面VAD⊥平面ABCD，F为AB中点。
（1）求VC与平面ABCD所成角的大小；
（2）当V到平面ABCD的距离为3时，求B到平面VFC的距离。
如图所示，ABCD是边长为a的正方形，△ABP是以角B为直角的等腰三角形．（1）H为BD上一点，且AH⊥平面PDB，求证：平面ABCD⊥平面APB；
（2）若PC=
| 3 |
如图所示，ABCD是边长为a的正方形，△PBA是以角B为直角的等腰三角形，H为BD上一点，且AH⊥平面PDB．（Ⅰ）求证：平面ABCD⊥平面APB；
（Ⅱ）求直线PC与平面PDB所成角的余弦值．
（2012•江西模拟）已知函数f（x）=Acos（ωx+φ）（A＞0，ω＞0，0＜φ＜π）为奇函数，该函数的部分图象如图所示，△EFG是边长1为的等边三角形，则f（1）的值为（ ）