摘要：设 .试求的值 座位号 17. 甲.乙两名射击运动员.甲射击一次命中10环的概率为.乙射击一次命中10环的概率为s.若他们各自独立地射击两次.设乙命中10环的次数为ξ.且ξ的数学期望Eξ=.表示甲与乙命中10环的次数的差的绝对值. (1)求s的值及的分布列. (2)求的数学期望. 18. 如图.已知ABCD是正方形.PD⊥平面ABCD.PD=AD. (1)求二面角A-PB-D的大小, (2)在线段PB上是否存在一点E,使PC⊥平面ADE?若存在,确定E点的位置,若不存在,说明理由. 座位号 21. 已知曲线C为顶点在原点.以x轴为对称轴.开口向右的抛物线.又点M(2.1)到抛物线C的准线的距离为. (1)求抛物线C的方程, (2)证明:过点M的任意一条直线与抛物线恒有公共点, 中的直线分别与抛物线C交于上下两点.又点的纵坐标依次成公差不为0的等差数列.试分析的大小关系. 湖南省2006届高三百校大联考第一次考试
网址：http://m.1010jiajiao.com/timu3_id_501832[举报]
，试求
的单调递减区间；
，试求
的值，使
到直线
距离的最小值为
；
对
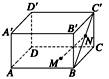
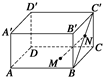
恒成立,求已知六面体ABCD—A′B′C′D′是平行六面体.
（1）化简
+
+
,并在图上标出其结果；
（2）设M是底面ABCD的中心，N是侧面BCC′B′对角线BC′上的
分点，设
=
+
+
，试求,,的值.
+
+
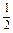
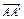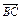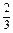
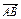,并在图上标出其结果；
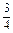分点，设 
=
+
，试求
的值
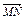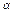
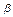
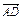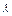
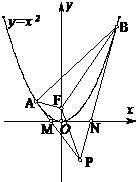（2012•安徽模拟）过抛物线y=x2上异于原点的任意两点A、B所作的两条切线交于点P，且交x轴于M、N（如图），F为抛物线的焦点．