摘要:设f(x)是定义域是R.且对一切实数x满足f, f, ; (2)已知时.求当时.函数g的表达式.并求出g(x)的最大值和最小值, =0的一根是0.记f(x)=0在区间[-1000.1000]上的根数为N.求N的最小值.
网址:http://m.1010jiajiao.com/timu3_id_501789[举报]
(本小题满分12 分)
分)
设函数f(x)的定义域为R,若|f(x)|≤|x|对任意的实数x均成立,则称函数f(x)为 函数。
函数。
(1)试判断函数 =
=
 =
= 中哪些是
中哪些是 函数,并说明理由;
函数,并说明理由;
(2)求证:若a>1,则函数f(x)=ln(x2+a)-lna是 函数。
函数。
(本小题满分12分)设函数f(x)的定义域是R,对于任意实数m,n,恒有f(m+n)=f(m)f(n),且当x>0时,0<f(x)<1。
(1)求证:f(0)=1,且当x<0时,有f(x)>1;
(2)判断f(x)在R上的单调性;
⑶设集合A={(x,y)|f(x2)f(y2)>f(1)},集合B={(x,y)|f(ax-y+2)=1,a∈R},若A∩B= ,求a的取值范围。
,求a的取值范围。
(本小题满分12分)
设函数f (x)=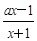 ,其中a∈R.
,其中a∈R.
(1)若a=1,f (x)的定义域为[0,3],求f (x)的最大值和最小值.
(2)若函数f (x)的定义域为区间(0,+∞),求a的取值范围使f (x)在定义域内是单调减函数.
查看习题详情和答案>>
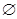 ,求a的取值范围。
,求a的取值范围。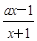 ,其中a∈R.
,其中a∈R.