摘要: 设数列{an}和{bn}满足a1=b1=6, a2=b2=4, a3=b3=3,且数列{an+1-an}(n∈N*)是等差数列,数列{bn-2}(n∈N*)是等比数列. (1)求数列{an}和{bn}的通项公式; (2)是否存在k∈N*,使ak-bk∈?若存在,求出k的值;若不存在,说明理由.
网址:http://m.1010jiajiao.com/timu3_id_501391[举报]
(本小题满分12分)
设{an}是公差不为O的等差数列,Sn是其前n项和,已知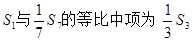 ,且
,且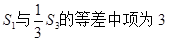
(1)求数列{an}的通项an
(2)求等比数列{bn}满足b1=S1 ,b2=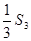 , 求和Tn=a1b1+a2b2+…+anbn
, 求和Tn=a1b1+a2b2+…+anbn
查看习题详情和答案>>
(本小题满分12分)
设{an}是公差不为O的等差数列,Sn是其前n项和,已知 ,且
,且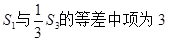
(1)求数列{an}的通项an
(2)求等比数列{bn}满足b1=S1 ,b2=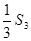 , 求和Tn=a1b1+a2b2+…+anbn
, 求和Tn=a1b1+a2b2+…+anbn
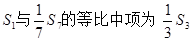 ,且
,且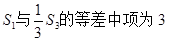
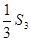 , 求和Tn=a1b1+a2b2+…+anbn
, 求和Tn=a1b1+a2b2+…+anbn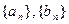 满足:
满足:
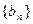 的通项公式;(2)设数列
的通项公式;(2)设数列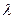 ,使得
,使得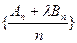 为等差数列?若存在,求出
为等差数列?若存在,求出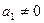 ,前n项和为Sn,且S4+a2=2S3;等比数列{bn}满足b1=a2,b2=a4
,前n项和为Sn,且S4+a2=2S3;等比数列{bn}满足b1=a2,b2=a4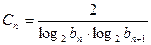 ,求数列{cn}的前n项的和Tn;
,求数列{cn}的前n项的和Tn;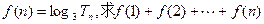 的最大值.
的最大值.