摘要： 设y=f(x)是定义在R上的任一函数.求证:为奇函数,G为偶函数,以任一定义在R上的函数为例.构造出一个奇函数和一个偶函数.
网址：http://m.1010jiajiao.com/timu3_id_501387[举报]
本题满分12分）
设f(x) 是定义在R上的减函数，满足f(x+y)=f(x)•f(y)且f(0)=1,数列{an}
满足a1=4，f(log3
f(-1-log3
=1
(n∈N*)；
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设Sn是数列{an}的前n项和, 试比较Sn与6n2-2的大小。
查看习题详情和答案>>
(本小题满分12分)已知函数f(x)=x2－1(x≥1)的图象是C1，函数y=g(x)的图象C2与C1关于直线y=x对称.
(1)求函数y=g(x)的解析式及定义域M；
(2)对于函数y=h(x)，如果存在一个正的常数a，使得定义域A内的任意两个不等的值x1，x2都有|h(x1)－h(x2)|≤a|x1－x2|成立，则称函数y=h(x)为A的利普希茨Ⅰ类函数.试证明：y=g(x)是M上的利普希茨Ⅰ类函数；
(3)设A、B是曲线C2上任意不同两点，证明：直线AB与直线y=x必相交.
(1)求函数y=g(x)的解析式及定义域M；
(2)对于函数y=h(x)，如果存在一个正的常数a，使得定义域A内的任意两个不等的值x1，x2都有|h(x1)－h(x2)|≤a|x1－x2|成立，则称函数y=h(x)为A的利普希茨Ⅰ类函数.试证明：y=g(x)是M上的利普希茨Ⅰ类函数；
(3)设A、B是曲线C2上任意不同两点，证明：直线AB与直线y=x必相交.
（本小题满分12分）已知函数y=f(x)在定义域（—1+∞）内满足f(o)=0，且f／(x)=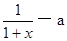 
，(f／(x))是f(x)的导数）
（Ⅰ）求f(x)的表达式.
（Ⅱ）当a=1时，讨论f(x)的单调性
（Ⅲ）设h(x)=（ex—P）2＋（x－P）2，证明：h(x)≥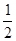
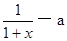，(f／(x))是f(x)的导数）（Ⅰ）求f(x)的表达式.
（Ⅱ）当a=1时，讨论f(x)的单调性
（Ⅲ）设h(x)=（ex—P）2＋（x－P）2，证明：h(x)≥
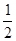
，求a的取值范围。
，求a的取值范围。