摘要:是否存在常数.使得不等式对任意正数恒成立 , 试证明你的结论. 在中.A.B.C分别为三个内角.a.b.c分别为其对边.外接圆半径为.已知, (Ⅰ)求角C ; (Ⅱ)求面积S的最大值 . 已知正项数列{an}和{bn}中.a1 = a ,(0<a<1=,b1=1-a,当n≥2且n∈时.an = an-1bn , bn =, (Ⅰ)证明:对任意n∈.都有an + bn = 1 (Ⅱ)求数列 {an} 的通项公式 (Ⅲ)设Cn = a·bn+1 , Sn为数列 {Cn} 的前n项和.求Sn 的值 如图.已知四棱锥P-ABCD中.面ABCD为正方形.PA⊥面ABCD.且PA = AB = a ,点M是PC的中点, (Ⅰ)求异面直线BP与MD所成角的大小, (Ⅱ)求二面角M-DA-C的大小. 已知直线l:与椭圆C:.且b为整数)交于M.N两点.B为椭圆C短轴的上端点.若ΔMBN的重心恰为椭圆焦点F. (Ⅰ)求椭圆C的方程, (Ⅱ)设椭圆C的左焦点为F’.问在椭圆C上是否存在一点P.使得∠F’PF = 60° ,证明你的结论. (Ⅲ)是否存在斜率不为零的直线l.使椭圆C与直线l相交于不同的两点R.S.且 |BR| = |BS|.如果存在.求直线l在y轴上截距的取值范围,如果不存在.请说明理由. 设x1.x2是函数f(x) = x3+x2-a2x 的两个极值点.且|x1|+|x2| = 2 (Ⅰ)证明:0<a≤1 ; (Ⅱ)证明:≤ ; = f′(x)-2a(x-x1),证明:当x1<x<2且x1<0时.|h(x)|≤4a .
网址:http://m.1010jiajiao.com/timu3_id_501370[举报]
(本小题满分12分)
已知定点 ,动点
,动点 满足:
满足:
 .
.
(I)求动点 的轨迹的方程;
的轨迹的方程;
(II)过点 的直线
的直线 与轨迹
与轨迹 交于两点
交于两点 ,试问在
,试问在 轴上是否存在定点
轴上是否存在定点 ,使得
,使得 为常数.若存在,求出点
为常数.若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看习题详情和答案>>
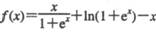 .
.
 时,
时,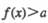 恒成立?若存在,求a的取值范围,若不存在,说明理由.
恒成立?若存在,求a的取值范围,若不存在,说明理由.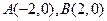 ,动点
,动点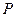 满足:
满足: 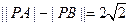 .
. 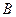 的直线
的直线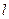 与轨迹
与轨迹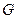 交于两点
交于两点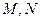 ,试问在
,试问在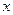 轴上是否存在定点
轴上是否存在定点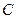 ,使得
,使得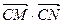 为常数.若存在,求出点
为常数.若存在,求出点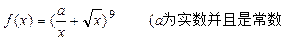 )
)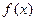 的展开式中
的展开式中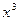 的系数为
的系数为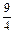 ,求常数
,求常数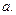
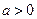 ,是否存在
,是否存在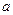 的值,使
的值,使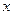 在定义域中取任意值时,
在定义域中取任意值时,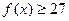 恒成立?如存在,求出
恒成立?如存在,求出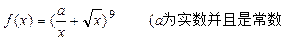 )
)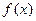 的展开式中
的展开式中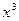 的系数为
的系数为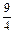 ,求常数
,求常数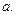
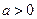 ,是否存在
,是否存在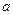 的值,使
的值,使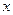 在定义域中取任意值时,
在定义域中取任意值时,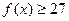 恒成立?如存在,求出
恒成立?如存在,求出